题目内容
已知正比例函数y=kx（k≠0）的函数值y随x的增大而增大，则一次函数y=x+k的图象大致是
A
解析试题分析：因为正比例函数y=kx（k≠0）的函数值y随x的增大而增大，可以判断k＞0；再根据k＞0判断出y=x+k的图象的大致位置．：∵正比例函数y=kx（k≠0）的函数值y随x的增大而增大，∴k＞0，∴一次函数y=x+k的图象经过一、三、二象限．故选A．
考点：本题考查了一次函数的性质和正比例函数的性质。
点评： 此类试题属于基础性很强的试题，但是很容易出错，主要是因为函数的性质问题，大致如下：主要考查了一次函数的图象性质，要掌握它的性质才能灵活解题．一次函数y=kx+b的图象有四种情况：①当k＞0，b＞0，函数y=kx+b的图象经过第一、二、三象限；②当k＞0，b＜0，函数y=kx+b的图象经过第一、三、四象限；③当k＜0，b＞0时，函数y=kx+b的图象经过第一、二、四象限；④当k＜0，b＜0时，函数y=kx+b的图象经过第二、三、四象限．
练习册系列答案
阅读快车系列答案
相关题目
已知正比例函数y=k1x（k1≠0）与反比例函数y=
（k2≠0）的图象有一个交点的坐标为（-2，-1），则它的另一个交点的坐标是（ ）
| k2 |
| x |
| A、（2，1） |
| B、（-2，-1） |
| C、（-2，1） |
| D、（2，-1） |
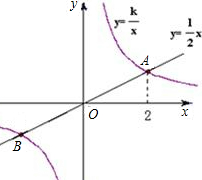横坐标为2．
如图，已知正比例函数和反比例函数的图象都经过点A（3，3）．