题目内容
【题目】已知二次函数![]() 的图像与直线
的图像与直线![]() 交于点
交于点![]() 、点
、点![]() .
.
(1)求![]() 的表达式和
的表达式和![]() 的值;
的值;
(2)当![]() 时,求自变量
时,求自变量![]() 的取值范围;
的取值范围;
(3)将直线![]() 沿
沿![]() 轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.
轴上下平移,当平移后的直线与抛物线只有一个公共点时,求平移后的直线表达式.
【答案】(1)![]() ,m=5;(2)x<-1或x>4;(3)平移后的直线为
,m=5;(2)x<-1或x>4;(3)平移后的直线为![]()
【解析】
(1)将A点代入二次函数解出b,将C点代入一次函数解出m;
(2)画出二次函数与一次函数图像,结合图像即可得到结果;
(3)设直线![]() 沿
沿![]() 轴平移n个单位,平移后的直线与抛物线一个公共点,即联立平移后的直线解析式与二次函数解析式,得到方程只有一个解,从而可得到n的值.
轴平移n个单位,平移后的直线与抛物线一个公共点,即联立平移后的直线解析式与二次函数解析式,得到方程只有一个解,从而可得到n的值.
(1)将![]() 代入
代入![]() ,得到0=1-b-3,解得b=-2
,得到0=1-b-3,解得b=-2
故二次函数解析式为![]()
![]() 代入
代入![]() ,得到m=4+1=5
,得到m=4+1=5
(2)由(1)可得二次函数解析式为![]() ,一次函数解析式为
,一次函数解析式为![]() ,在直角坐标系中画出两个函数图像如图:
,在直角坐标系中画出两个函数图像如图:
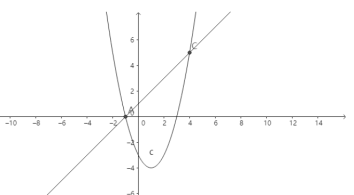
结合图像可知当![]() 时,x<-1或x>4
时,x<-1或x>4
(3)设直线![]() 沿
沿![]() 轴平移n个单位,平移后的直线解析式为y3=x+1+n,与二次函数
轴平移n个单位,平移后的直线解析式为y3=x+1+n,与二次函数![]() 只有一个交点,故
只有一个交点,故![]() 有且只有一个解,
有且只有一个解,
将方程变形得到![]() ,△=(-3)2+4(4+n)=0,解得n=
,△=(-3)2+4(4+n)=0,解得n=![]()
所以平移后的直线为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目