题目内容
如图在正方形ABCD中点E是CD的中点，AC与BE相交于点F，连接DF并延长交BC于点G，连接AE交DG于点H，则下列结论：①△ADF≌△ABF；②GB=GC；③S△ABF=S△GBF；④DE2=EH•EB，其中结论正确的个数是（ ）| A、1 | B、2 | C、3 | D、4 |
考点：相似三角形的判定与性质,全等三角形的判定与性质
专题：
分析：根据题意结合图形，灵活运用有关定理对每一个结论逐一解析，即可解决问题．
解答：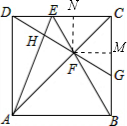
解：如图，过点F作FM⊥BC，FN⊥DC；
∵四边形ABCD是正方形，
∴∠DAF=∠BAF=45°，AD=AB=BC=CD；
∴FM=FN
在△ADF与△ABF中，
，
∴△ADF≌△ABF（SAS），
故①正确；
∵四边形ABCD是正方形，
∴DC∥AB，BC∥AD；
∴△CEF∽△ABF，△CGF∽△ADF，
∴
=
，
=
，而AB=AD，
∴CE=CG=
BC，
∴BG=CG，故②正确；
∵△CEF∽△ABF，
∴
=(
)2=
；
∵CE=BG，FM=FN，
∴S△CEF=S△BGF，
故③不正确；
∵四边形ABCD是正方形，
∴AD=BC，∠EDA=∠ECB；
在△ADE与△BCE中，
，
∴△ADE≌△BCE（SAS），
∴AE=BE；
同理可证：△ADE≌△DCG，
∴AE=DG；∠DAE=∠CDG，
∵∠DAE+∠DEA=90°，
∴∠CDG+∠DEA=90°，
∴∠EDH=90°，
∴DE2=EH•AE，而EA=EB，
∴DE2=EH•EB．
故④正确．
综上所述，正确结论有3个．
故选C．
解：如图，过点F作FM⊥BC，FN⊥DC；∵四边形ABCD是正方形，
∴∠DAF=∠BAF=45°，AD=AB=BC=CD；
∴FM=FN
在△ADF与△ABF中，
|
∴△ADF≌△ABF（SAS），
故①正确；
∵四边形ABCD是正方形，
∴DC∥AB，BC∥AD；
∴△CEF∽△ABF，△CGF∽△ADF，
∴
| CE |
| AB |
| CF |
| AF |
| CG |
| AD |
| CF |
| AF |
∴CE=CG=
| 1 |
| 2 |
∴BG=CG，故②正确；
∵△CEF∽△ABF，
∴
| S△CEF |
| S△ABF |
| CE |
| AB |
| 1 |
| 4 |
∵CE=BG，FM=FN，
∴S△CEF=S△BGF，
故③不正确；
∵四边形ABCD是正方形，
∴AD=BC，∠EDA=∠ECB；
在△ADE与△BCE中，
|
∴△ADE≌△BCE（SAS），
∴AE=BE；
同理可证：△ADE≌△DCG，
∴AE=DG；∠DAE=∠CDG，
∵∠DAE+∠DEA=90°，
∴∠CDG+∠DEA=90°，
∴∠EDH=90°，
∴DE2=EH•AE，而EA=EB，
∴DE2=EH•EB．
故④正确．
综上所述，正确结论有3个．
故选C．
点评：该题以正方形为载体，主要考查了全等三角形的判定及其性质、相似三角形的判定及其性质等几何知识点的应用问题；对综合的分析问题解决问题的能力提出了较高的要求．
练习册系列答案
相关题目
在Rt△ABC中，∠C=90°，AB=3，AC=2，则cosB=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在-
，-|-6|，-（-5），-32，（-1）2，20%，0这七个数中，正数的个数有（ ）
| 2 |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
下面的多项式中，能分解因式的是（ ）
A、m2-m+
| ||
| B、m2+2m+4 | ||
C、m2-m+
| ||
| D、m2-2m+2 |