题目内容
2.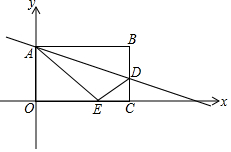 以矩形OABC的OC边所在直线为x轴,OA边所在直线为y轴建立平面直角坐标系如图所示,已知OA=8,OC=10,将矩形OABC沿直线AD折叠,点B恰好落在x轴上的点E处.
以矩形OABC的OC边所在直线为x轴,OA边所在直线为y轴建立平面直角坐标系如图所示,已知OA=8,OC=10,将矩形OABC沿直线AD折叠,点B恰好落在x轴上的点E处.(1)求点E的坐标;
(2)求直线AD的解析式;
(3)x轴上是否存在一点P,使得△PAD的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
分析 (1)利用勾股定理求OE的长可得E的坐标;
(2)先根据折叠设未知数,利用勾股定理列方程可求CD的长,得D的坐标,利用待定系数法求直线AD的解析式;
(3)根据轴对称的最短路径,作A关于点O的对称点A'(0,-8),连接A'D交x轴于P,此时△PAD的周长最小,利用待定系数法求直线A‘D的解析式,令y=0代入可得P的坐标.
解答  解:(1)由折叠得:AB=AE=10,
解:(1)由折叠得:AB=AE=10,
∵∠AOC=90°,OA=8,
∴OE=6,
∵E(6,0);
(2)EC=OC-OE=10-6=4,
设DB=x,则DE=BD=x,DC=8-x,
Rt△EDC中,由勾股定理得:DE2=DC2+EC2,
∴x2=(8-x)2+42,
x=5 ,
,
∴DC=8-5=3,
∵D(10,3),
设直线AD的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{10k+b=3}\\{b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=8}\end{array}\right.$,
∴直线AD的解析式为:y=-$\frac{1}{2}$x+8;
(3)存在,作A关于点O的对称点A'(0,-8),
连接A'D交x轴于P,此时△PAD的周长最小,
设直线A'D的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{10k+b=3}\\{b=-8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{11}{10}}\\{b=-8}\end{array}\right.$,
∴直线AD的解析式为:y=$\frac{11}{10}$x-8;
当y=0时,x=$\frac{80}{11}$,
∴P($\frac{80}{11}$,0).
点评 本题是四边形的综合题,考查了矩形的性质、图形与坐标特点、勾股定理、折叠的性质、利用待定系数法求直线的解析式;难度适中,熟练掌握折叠的性质是关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 4 | B. | $\sqrt{10}$ | C. | 2$\sqrt{2}$ | D. | 10 |
 如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )
如图,在平面直角坐标系中,A(0,0)、B(4,0)、D(1,2)为平行四边形的三个顶点,则第四个顶点C的坐标是( )| A. | (2,5) | B. | (4,2) | C. | (5,2) | D. | (6,2) |
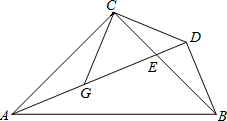 如图,△ABC中,AC=BC,∠ACB=90°,点D在△ABC的外部,且AD⊥BD,AD交BC于点E,连结CD,过点C作CG⊥CD,交AD于点G.
如图,△ABC中,AC=BC,∠ACB=90°,点D在△ABC的外部,且AD⊥BD,AD交BC于点E,连结CD,过点C作CG⊥CD,交AD于点G.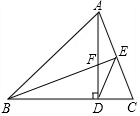 如图,在Rt△BDF中,∠BDF=90°,把△BDF绕点D顺时针旋转90°,使点B和点F分别落在DF、BD的延长线上的点A和点C处,延长BF与AC交于点E,连接AB、DE.
如图,在Rt△BDF中,∠BDF=90°,把△BDF绕点D顺时针旋转90°,使点B和点F分别落在DF、BD的延长线上的点A和点C处,延长BF与AC交于点E,连接AB、DE.