题目内容
把二次函数y=5x2的图象先向左平移3个单位,再向下平移2个单位后,所得二次函数图象的解析式是( )
| A、y=5(x+3)2-2 |
| B、y=5(x+3)2+2 |
| C、y=5(x-3)2-2 |
| D、y=5(x-3)2-2 |
考点:二次函数图象与几何变换
专题:
分析:先利用顶点式得到抛物线y=5x2的顶点坐标为(0,0),再根据点平移的规律得到点(0,0)平移后所得对应点的坐标为(-3,-2),然后根据顶点式写出平移后的抛物线的解析式.
解答:解:抛物线y=5x2的顶点坐标为(0,0),点(0,0)向左平移3个单位,再向下平移个单位所得对应点的坐标为(-3,-2),所以平移后的抛物线的解析式为y=5(x+3)2-2.
故选A.
故选A.
点评:本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.

练习册系列答案
相关题目
下列说法正确的是( )
| A、x2+3x=0是二项方程 | ||||
| B、xy-2y=2是二元二次方程 | ||||
C、
| ||||
D、
|
 如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠AOD=100°,则∠B的度数为( )
如图,AB与CD交于点O,OA=OC,OD=OB,∠A=50°,∠AOD=100°,则∠B的度数为( )| A、50° | B、30° |
| C、80° | D、100° |

 如图,图中已标出的8个角中,同位角、内错角、同旁内角各有几对?
如图,图中已标出的8个角中,同位角、内错角、同旁内角各有几对?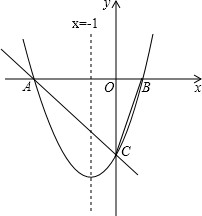 对称轴为直线x=-1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(-3,0).
对称轴为直线x=-1的抛物线y=x2+bx+c,与x轴相交于A,B两点,其中点A的坐标为(-3,0). 观察图形并填空.
观察图形并填空.