题目内容
7.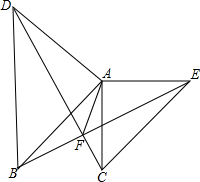 如图,在△ABD中,AD=AB,∠DAB=90°,在△ACE中,AC=AE,∠EAC=90°,CD,BE相交于点F.求证:
如图,在△ABD中,AD=AB,∠DAB=90°,在△ACE中,AC=AE,∠EAC=90°,CD,BE相交于点F.求证:(1)DC=BE,且DC⊥BE;
(2)FA平分∠DFE.
分析 (1)由△ABD和△ACE都是等腰直角三角形得出AB=AD,AE=AC,∠BAD=∠CAE=90°,再进一步得出∠DAC=∠BAE证得△ABE≌△ADC,得出结论;
(2)由∠DAB=∠DFB=90°,推出A,D,B,F四点共圆,根据圆周角定理得到∠AFD=∠ABD=45°于是得到∠DFA=$\frac{1}{2}∠$DFE,即可得到结论.
解答 证明:(1)∵△ABD和△ACE都是等腰直角三角形,
∴AB=AD,AE=AC,
又∵∠BAD=∠CAE=90°,
∴∠BAD+∠BAC=∠CAE+∠BAC,
即:∠DAC=∠BAE,
在△ABE和△ADC中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AE=AC}\end{array}\right.$,
∴△ABE≌△ADC(SAS)
∴BE=DC,∠ADF=∠ABF,
∵∠ADF+∠FDB+∠DBA=90°,
∴∠FDB+∠DBA+∠ABF=90°,
∴∠DFB=90°,
∴CD⊥BE;
(2)∵∠DAB=∠DFB=90°,
∴A,D,B,F四点共圆,
∴∠AFD=∠ABD=45°
∵CD⊥BE,
∴∠DFA=$\frac{1}{2}∠$DFE,
∴FA平分∠DFE.
点评 此题考查了全等三角形的判定与性质,等腰直角三角形的性质,四点共圆,圆周角定理,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 选取合适的比例,画出如图所示物体的三视图.单位:mm.
选取合适的比例,画出如图所示物体的三视图.单位:mm. 如图,在平面直角坐标系中,O是原点,已知A(4,3),P是y轴上的动点,当点O,A,P三点组成的三角形为等腰三角形时,求出所有符合条件的点P坐标.
如图,在平面直角坐标系中,O是原点,已知A(4,3),P是y轴上的动点,当点O,A,P三点组成的三角形为等腰三角形时,求出所有符合条件的点P坐标. 已知∠AOB=80°,OE,OC分别平分∠AOD与∠BOD,∠COD=15°,求∠DOE的度数.
已知∠AOB=80°,OE,OC分别平分∠AOD与∠BOD,∠COD=15°,求∠DOE的度数.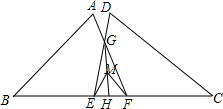 如图,点E,F在BC上,AF,DE相交于点G,H为EF中点,BE=CF,AB=DC,∠B=∠C,判断△MEF形状,请说明你的理由.
如图,点E,F在BC上,AF,DE相交于点G,H为EF中点,BE=CF,AB=DC,∠B=∠C,判断△MEF形状,请说明你的理由.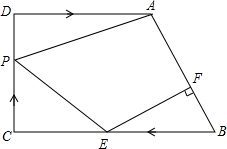 如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)
如图,在梯形ABCD中,AD∥BC,∠C=90°,AD=8cm,CD=6cm,BC=10cm,点P以每秒1cm的速度从点C出发沿CD向点D运动,同时点E以每秒2cm的速度从点B出发沿BC向点C运动,过点E作EF⊥AB,交AB于点F,连接PA,PE,设运动时间为t秒.(0<t<5)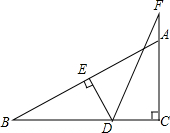 如图.已知∠ACB=90°,AD平分∠BAC交BC于D,DE⊥AB于E,BD=DF交CA的延长线于F点,求证:BE=AE+AF.
如图.已知∠ACB=90°,AD平分∠BAC交BC于D,DE⊥AB于E,BD=DF交CA的延长线于F点,求证:BE=AE+AF. 如图,观察图(1)中三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有7个面,10个顶点,15条棱…由此推得
如图,观察图(1)中三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有7个面,10个顶点,15条棱…由此推得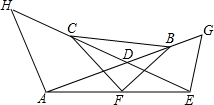 如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.