题目内容
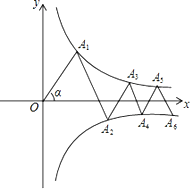
【题目】如图,![]() 为线段
为线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),在线段
重合),在线段![]() 的同侧分别作等边
的同侧分别作等边![]() 和等边
和等边![]() ,连结
,连结![]() 、
、![]() ,交点为
,交点为![]() .若
.若![]() ,求动点
,求动点![]() 运动路径的长为( )
运动路径的长为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
根据题意分析得出点Q运动的轨迹是以AB为弦的一段圆弧,当点P运动到AB的中点处时PQ取得最大值,过点P作OP⊥AB,取AQ的中点E作OE⊥AQ交PQ于点O,连接OA,设半径长为R,则根据勾股定列出方程求出R的值,再根据弧长计算公式l=![]() 求出l值即可.
求出l值即可.
解:依题意可知,点Q运动的轨迹是以AB为弦的一段圆弧,当点P运动到AB的中点处时PQ取得最大值,如图所示,连接PQ,取AQ的中点E作OE⊥AQ交直线PQ于点O,连接OA,OB.
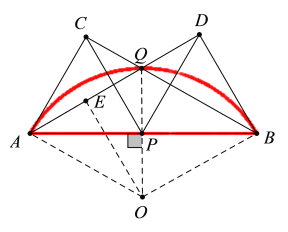
∵P是AB的中点,
∴PA=PB=![]() AB=
AB=![]()
![]() 6=3.
6=3.
∵![]() 和
和![]() 是等边三角形,
是等边三角形,
∴AP=PC,PB=PD,∠APC=∠BPD=60°,
∴AP=PD,∠APD=120°.
∴∠PAD=∠ADP=30°,
同理可证:∠PBQ=∠BCP=30°,
∴∠PAD=∠PBQ.
∵AP=PB,
∴PQ⊥AB.
∴tan∠PAQ=![]() =
=![]()
∴PQ=![]() .
.
在Rt△AOP中,
![]()
即![]()
解得:OA=![]() .
.
∵sin∠AOP=![]() =
=![]() =
=![]()
∴∠AOP=60°.
∴∠AOB=120°.
∴l=![]() =
=![]() =
=![]() .
.
故答案选B.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目