题目内容
10.我们知道同一平面内的两条直线有相交和平行两种位置关系.(1)观察与思考:如图1,若AB∥CD,点P在AB、CD内部,∠BPD、∠B、∠D之间的数量关系为∠BPD=∠B+∠D,不必说明理由;
(2)猜想与证明:如图2,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,利用(1)中的结论(可以直接套用)求∠BPD、∠B、∠D、∠BQD之间有何数量关系?并证明你的结论;
(3)拓展与应用:如图3,设BF交AC于点M,AE交DF于点N,已知∠AMB=140°,∠ANF=105°.利用(2)中的结论直接写出∠B+∠E+∠F的度数为75度,∠A比∠F大65度.

分析 (1)过点P作PE∥AB,根据两直线平行,内错角相等可得∠B=∠1,∠D=∠2,再根据∠BPD=∠1+∠2即可得解;
(2)连接QP并延长,再根据三角形的一个外角等于与它不相邻的两个内角的和解答;
(3)依据(2)中的结论、三角形的内角和及三角形的外角和即可求得.
解答  解:(1)过点P作PE∥AB,
解:(1)过点P作PE∥AB,
∵AB∥CD,
∴AB∥EP∥CD,
∴∠B=∠1,∠D=∠2,
∴∠BPD=∠B+∠D;
(2)如图,连接QP并延长,
结论:∠BPD=∠BQD+∠B+∠D.
∠BPD=(∠BQP+∠B)+(∠DQP+∠D)=∠BQD+∠B+∠D.
(3)∵∠ANF=105°,
∴∠ENF=∠B+∠E+∠F=180°-105°=75°,
∵∠A=∠AMB-∠B-∠E,
∠F=180°-∠ANF-∠B-∠E,
∴∠A-∠F=∠AMB+∠ANF-180°=65°.
故答案为:∠BPD=∠B+∠D;75,65.
点评 本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记性质并作出辅助线是解题的关键.

练习册系列答案
相关题目
15.在$-\sqrt{3}$,π,$\frac{13}{3}$,0,$\root{3}{-27}$,$-2.\stackrel{••}{37}$,0.585085008…(5和8之间依次多1个0),这7个数中,无理数共有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
20.下列说法正确的是( )
| A. | 5是25的算术平方根 | B. | 16是4的算术平方根 | ||
| C. | -6是(-6)2的算术平方根 | D. | 0没有算术平方根 |
 如图,?ABCD的对角线AC、BD交于点O,AB=5,OA=3,OB=4,则?ABCD的周长是多少?
如图,?ABCD的对角线AC、BD交于点O,AB=5,OA=3,OB=4,则?ABCD的周长是多少?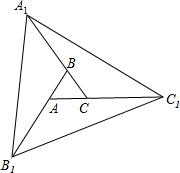 如图,把面积为1的等边△ABC的三边分别向外延长m倍,得到△A1B1C1,那么△A1B1C1的面积是3m2+3m+1(用含m的式子表示)
如图,把面积为1的等边△ABC的三边分别向外延长m倍,得到△A1B1C1,那么△A1B1C1的面积是3m2+3m+1(用含m的式子表示) 如图是由四个全等的直角三角形拼成的一个中空的大正方形,已知直角三角形的两条直角边长分别为11cm和7cm,求整个大正方形的面积.
如图是由四个全等的直角三角形拼成的一个中空的大正方形,已知直角三角形的两条直角边长分别为11cm和7cm,求整个大正方形的面积. 已知:线段a和∠α
已知:线段a和∠α