��Ŀ����
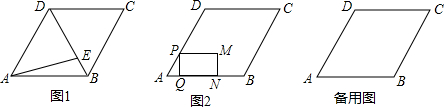
3����ͼ1������ABCD�ı߳�Ϊ6����ABC=120�㣮����P�ӵ�A ���������߶�AD-DC����ÿ��1����λ���ȵ��ٶ���C���˶������P���˶�ʱ��Ϊt�루t��0������1��������ABCD�������
��2����ͼ1����E�ڶԽ���BD����DE=2EB������AE���ڵ�P��A�㵽C���˶������У��Ƿ���ڡ�AEP��ֱ�������ε�ʱ�̣������ڣ��������Ӧ��t��ֵ���������ڣ���˵�����ɣ�
��3����ͼ2������P��PQ��AB ��Q�㣬��PQΪһ�ߣ�PMΪ��һ������������PQNM������PM=4�����˶������е�Q����B���غ�ʱ�˶�ֹͣ�������PQNM������ABCD�غϲ��ֵ����ΪS��ֱ��д��S��t֮��ĺ�����ϵʽ�����Ӧ���Ա�����ȡֵ��Χ��
���� ��1��������ABCD�ı߳�Ϊ6����ABC=120�㣬֪���ε�������ڵȱ�������ABD�����2����
��2�����ڣ�EP��ADʱ����P��AD�ϻ�PE��AEʱ����P��DC�ϣ��ù��ɶ��������������ƽ����
��3������������������ۣ���0��t��4����4��t��3$\sqrt{3}$����3$\sqrt{3}$��t��8����8��t��9��
��� �⣺��1��������ABCD�ı߳�Ϊ6����ABC=120��
��S����ABCD=2S��ABD=$\frac{1}{2}��6��3\sqrt{3}$=9$\sqrt{3}$�� ��2�����ڣ�
��2�����ڣ�
��EP��ADʱ����P��AD�ϣ���ͼ1����EP��AD��
��DE=$\frac{2}{3}$BD=4����ADB=60�㣬
��PD=2��AP=4��
��t=4��
��PE��AEʱ����P��DC�ϣ���ͼ2����PE��AE��AG��BD��PF��BD��
��PD=t-6����PDB=60�㣬
��PF=$\sqrt{3}$��t-6����DF=$\frac{t-6}{2}$��
��EF=4-$\frac{t-6}{2}$=$\frac{14-t}{2}$��
��AG=3$\sqrt{3}$��DG=3��
��GE=1
�ߡ�AGE�ס�EFP��
��$\frac{PF}{EG}=\frac{EF}{AG}$��
��$\frac{\sqrt{3}��t-6��}{1}=\frac{\frac{14-t}{2}}{3\sqrt{3}}$��
��ã�t=$\frac{86}{13}$��
��3���ٵ�0��t��4ʱ��S=2$\sqrt{3}$t��
�ڵ�4��t��3$\sqrt{3}$ʱ��S=2$\sqrt{3}$t-$\frac{\sqrt{3}��t-4��^{2}}{8}$=-$\frac{\sqrt{3}}{8}$t2+3$\sqrt{3}$t-2$\sqrt{3}$��
�۵�3$\sqrt{3}$��t��8ʱ��S=12$\sqrt{3}$-$\frac{\sqrt{3}��t-5��^{2}}{2}$=-$\frac{\sqrt{3}}{2}$t2+5$\sqrt{3}$t-$\frac{\sqrt{3}}{2}$��
�ܵ�8��t��9ʱ��S=12$\sqrt{3}$-$\frac{1}{2}$��[��t-5��+��t-8��]��3$\sqrt{3}$=-3$\sqrt{3}$t+$\frac{63\sqrt{3}}{2}$��
���� ���⿼���˼��α任�еĶ������⣬�漰�������ε����ʣ��ȱ������ε��ж������ʣ����ɶ��������Ǻ����������ε����Ƶ��ж������ʣ������������Ĺؼ����ܷ��������������λ�ã����������������ز�©������˼����

 �ƸԴ��ž�ϵ�д�
�ƸԴ��ž�ϵ�д�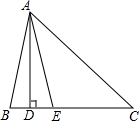 ��ͼ����ABC�У�AD��BC��AEƽ�֡�BAC��
��ͼ����ABC�У�AD��BC��AEƽ�֡�BAC�� ��ͼ���ڿ�ǽ��ǽ��Ϊ20m���ĵط�Χ��һ�����ε����������������������Χ�ɣ����������ܳ�Ϊ18m�������Ŀ���m���볤��m���ĺ�������ʽΪy=$9-\frac{x}{2}$�������Ϊ2m����ô��Ϊ14��
��ͼ���ڿ�ǽ��ǽ��Ϊ20m���ĵط�Χ��һ�����ε����������������������Χ�ɣ����������ܳ�Ϊ18m�������Ŀ���m���볤��m���ĺ�������ʽΪy=$9-\frac{x}{2}$�������Ϊ2m����ô��Ϊ14��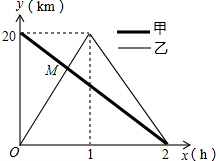 ��һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱ��x��h��֮��ĺ���ͼ����ͼ�����������⣺
��һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�أ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱ��x��h��֮��ĺ���ͼ����ͼ�����������⣺