题目内容
已知4x2+y2-4x-6y+10=0,求( +y2
+y2 )-(x2
)-(x2 -5x
-5x )的值.
)的值.
解:4x2+y2-4x-6y+10=0变形得:
4(x- )2+(y-3)2=0,
)2+(y-3)2=0,
则x- =0且y-3=0,
=0且y-3=0,
解得:x= ,y=3,
,y=3,
则原式=(2x +
+ )-(x
)-(x -5
-5 )
)
=2x +
+ -x
-x +5
+5
=x +6
+6
= ×
×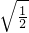 +6×
+6×
= +3
+3 .
.
分析:将已知等式左边利用完全平方公式配方变形后,根据两个非负数之和为0,两非负数分别为0求出x与y的值,将所求式子利用二次根式的化简公式化简后,去括号合并同类二次根式后,将x与y的值代入即可求出值.
点评:此题考查了二次根式的化简,配方法的应用,以及非负数的性质:偶次方,其中求出x与y的值是本题的突破点.
4(x-
 )2+(y-3)2=0,
)2+(y-3)2=0,则x-
 =0且y-3=0,
=0且y-3=0,解得:x=
 ,y=3,
,y=3,则原式=(2x
 +
+ )-(x
)-(x -5
-5 )
)=2x
 +
+ -x
-x +5
+5
=x
 +6
+6
=
 ×
×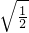 +6×
+6×
=
 +3
+3 .
.分析:将已知等式左边利用完全平方公式配方变形后,根据两个非负数之和为0,两非负数分别为0求出x与y的值,将所求式子利用二次根式的化简公式化简后,去括号合并同类二次根式后,将x与y的值代入即可求出值.
点评:此题考查了二次根式的化简,配方法的应用,以及非负数的性质:偶次方,其中求出x与y的值是本题的突破点.

练习册系列答案
相关题目
 y的值.
y的值. +y2
+y2 )-(x2
)-(x2 -5x
-5x )的值。
)的值。 +y2
+y2 )-(x2
)-(x2 -5x
-5x )的值.
)的值.