题目内容
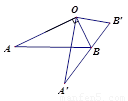
如图,∠AOB=90º,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanA= ,OB=5,则BB′=
.
,OB=5,则BB′=
.
【答案】
 .
.
【解析】
试题分析:根据旋转的性质得出△OAB≌△OA′B′,则有OB=OB′.过O作OD⊥BB′,则D为BB′的中点,易求DB′= ,故BB′=
,故BB′= .
.
试题解析:根据旋转得△OAB≌△OA′B′,
∴OB=OB′,∠ABO=∠B′,
过O作OD⊥BB′,则D为BB′的中点,∠B′OD=∠A

∴
设 ,则
,则
∵
∴
解得: 或
或 (舍去)
(舍去)
∴ .
.
考点: 旋转的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

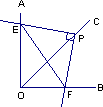
 角度得到的,若点A’在AB上,,则旋转角
角度得到的,若点A’在AB上,,则旋转角
