题目内容
6.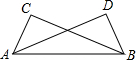 如图,已知∠CAB=∠DBA,添加一个条件使△CAB≌△DBA,以下错误的是( )
如图,已知∠CAB=∠DBA,添加一个条件使△CAB≌△DBA,以下错误的是( )| A. | ∠CBA=∠DAB | B. | ∠C=∠D | C. | AC=BD | D. | CB=DA |
分析 根据全等三角形的判定:SAS,AAS,ASA,可得答案.
解答 解:由题意,得∠CAB=∠DBA,AB=BA,
A、在△CAB与△DBA中,$\left\{\begin{array}{l}{∠CAB=∠DBA}\\{AB=BA}\\{∠CBA=∠DAB}\end{array}\right.$,△CAB≌△DBA(ASA),故本选项正确;
B、在△CAB与△DBA中,$\left\{\begin{array}{l}{∠C=∠D\\}\\{∠CAB=∠DBA}\\{AB=BA}\end{array}\right.$,△CAB≌△DBA(AAS),故本选项正确;
C、在△CAB与△DBA中,$\left\{\begin{array}{l}{AC=BD}\\{∠CAB=∠DBA}\\{AB=BA}\end{array}\right.$,△CAB≌△DBA(SAS),故本选项正确;
D、∠CAB=∠DBA,AB=BA,CB=DA,(SSA)三角形不全等,故本选项错误时;
故选:D.
点评 本题考查了全等三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角

练习册系列答案
相关题目
5. 某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
(1)图表中的m=16,n=30;
(2)扇形统计图中F组所对应的圆心角为18度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?
 某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:
某校为了解学生的每周平均课外阅读时间,在本校随机抽取若干名学生进行调查,并将调查结果绘制成如下不完整的统计图表,请根据图表中所给的信息,解答下列问题:| 组别 | 阅读时间t(单位:小时) | 频数(人数) |
| A | 0≤t<1 | 8 |
| B | 1≤t<2 | 20 |
| C | 2≤t<3 | 24 |
| D | 3≤t<4 | m |
| E | 4≤t<5 | 8 |
| F | t≥5 | 4 |
(2)扇形统计图中F组所对应的圆心角为18度;
(3)该校共有学生1500名,请估计该校有多少名学生的每周平均课外阅读时间不低于3小时?
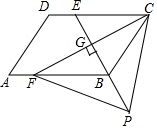 如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有①②③④.(填序号)
如图,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,下列结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确的有①②③④.(填序号)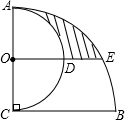 如图,AC⊥BC,AC=BC=6,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$.过点O作BC的平行线交两弧于D、E,则阴影部分的面积是$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$.
如图,AC⊥BC,AC=BC=6,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作$\widehat{AB}$.过点O作BC的平行线交两弧于D、E,则阴影部分的面积是$\frac{15}{4}$π-$\frac{9\sqrt{3}}{2}$.