题目内容
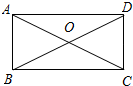如图在矩形ABCD中，对角线AC、BD相交于点O，∠BOC=120°，AB=6，求：（1）对角线的长；
（2）BC的长；
（3）矩形ABCD的面积．
考点：矩形的性质,勾股定理
专题：
分析：（1）根据矩形的性质和等边三角形的判定定理得到△AOB是等边三角形，则OB=AB=6，故BD=2OB=12；
（2）在直角△ABC中，利用勾股定理来求BC的长度；
（3）根据“矩形的面积=长×宽”进行解答．
（2）在直角△ABC中，利用勾股定理来求BC的长度；
（3）根据“矩形的面积=长×宽”进行解答．
解答：解：（1）∵四边形ABCD是矩形，
∴OA=OB=
BD．
又∵∠BOC=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OB=AB=6，
∴对角线BD的长度是：BD=2OB=12；
（2）由（1）知，矩形ABCD的对角线长是12，则AC=12．
在直角△ABC中，AB=6，AC=12，则由勾股定理得到：BC=
=6
；
（3）在矩形ABCD中，AB=6，BC=6
，则该矩形的面积=AB•BC=6×6
=36
．
解：（1）∵四边形ABCD是矩形，∴OA=OB=
| 1 |
| 2 |
又∵∠BOC=120°，
∴∠AOB=60°，
∴△AOB是等边三角形，
∴OB=AB=6，
∴对角线BD的长度是：BD=2OB=12；
（2）由（1）知，矩形ABCD的对角线长是12，则AC=12．
在直角△ABC中，AB=6，AC=12，则由勾股定理得到：BC=
| AC2-AB2 |
| 3 |
（3）在矩形ABCD中，AB=6，BC=6
| 3 |
| 3 |
| 3 |
点评：本题考查了矩形的性质、勾股定理．解题的关键是根据已知条件判定△AOB是等边三角形．
练习册系列答案
相关题目
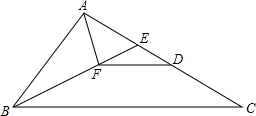已知如图，点E在△ABC的边AC上，且∠AEB=∠ABC．