题目内容
矩形的一条角平分线分对边为3和4两部分，则矩形周长为 ．
考点：矩形的性质
专题：
分析：根据矩形的性质得出AD=BC，AB=CD，AD∥BC，推出∠AEB=∠CBE，求出∠ABE=∠CBE=∠AEB，推出AB=AE=CD，分为两种情况，代入求出即可．
解答：解：
∵四边形ABCD是矩形，
∴AD=BC，AB=CD，AD∥BC，
∴∠AEB=∠CBE，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠AEB=∠ABE，
∴AB=AE，
当AE=3时，AB=AE=3=CD，AD=3+4=7=BC，
∴此时矩形ABCD的周长是AB+BC+CD+AD=3+3+7+7=20；
当AE=4时，AB=AE=4=CD，AD=3+4=7=BC，
∴此时矩形ABCD的周长是AB+BC+CD+AD=4+4+7+7=22；
故答案是：20或22．
∵四边形ABCD是矩形，∴AD=BC，AB=CD，AD∥BC，
∴∠AEB=∠CBE，
∵BE平分∠ABC，
∴∠ABE=∠CBE，
∴∠AEB=∠ABE，
∴AB=AE，
当AE=3时，AB=AE=3=CD，AD=3+4=7=BC，
∴此时矩形ABCD的周长是AB+BC+CD+AD=3+3+7+7=20；
当AE=4时，AB=AE=4=CD，AD=3+4=7=BC，
∴此时矩形ABCD的周长是AB+BC+CD+AD=4+4+7+7=22；
故答案是：20或22．
点评：本题考查了矩形的性质，平行线的性质，等腰三角形的判定等知识点，关键是求出AB的长，注意要进行分类讨论．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
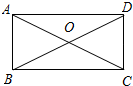如图在矩形ABCD中，对角线AC、BD相交于点O，∠BOC=120°，AB=6，求：
如图，AB、CD相交于点O，OB平分∠DOE，若∠DOE=60°，求∠AOC的度数．
如图所示，AB是圆中的一条弦，C是圆上（不同于A、B）的点，过B的切线与AC的延长线交于P点，Q是
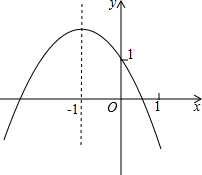已知二次函数y=ax2+bx+c的图象如图所示，有以下结论：