题目内容
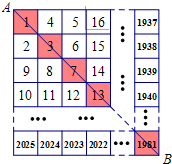 (2012•南浔区二模)如图,将1~2025这2025个自然数按图中规律分别排列在网格中,除对角线AB经过的45个数外,其它的数被分成两部分,对角线AB右上方的990个数之和记为S1,对角线AB左下方的990个数之和记为S2.则S1-S2=
(2012•南浔区二模)如图,将1~2025这2025个自然数按图中规律分别排列在网格中,除对角线AB经过的45个数外,其它的数被分成两部分,对角线AB右上方的990个数之和记为S1,对角线AB左下方的990个数之和记为S2.则S1-S2=-1012
-1012
.分析:按照数据的排列,求出对角线上的数向上的所有数的和与向左的所有的数的和的差,从而得到右上角的所有的数的和减去左下角的所有的数的和的算式,再根据数据的特点先求出出相邻两数的和,从而发现后一个数比前一个数小4,再根据等差数列求和公式列式计算即可得解.
解答:解:以对角线上的第2个数3为标准,4-2=2=1×2,
以对角线上的第3个数7为标准,(5+6)-(8+9)=(5-8)+(6-9)=-2×3,
以对角线上的第4个数13为标准,(14+15+16)-(12+11+10)=(14-10)+(15-11)+(16-12)=3×4,
以对角线上的第5个数21为标准,(17+18+19+20)-(22+23+24+25)=(17-22)+(18-23)+(19-24)+(20-25)=-4×5,
…,
以对角线上的第45个数1981为标准,(1937+1938+…+1980)-(1982+1983+…+2025)=(1937-1982)+(1938-1983)+…+(1980-2025)=-44×45,
所以S1-S2=1×2-2×3+3×4-4×5+…+43×44-44×45
=2(1-3)+4×(3-5)+…+44×(43-45)
=-4-8-…-88
=-(4+8+12+…+88)
=-
×(4+88)×
=-
×92×22
=-1012.
故答案为:-1012.
以对角线上的第3个数7为标准,(5+6)-(8+9)=(5-8)+(6-9)=-2×3,
以对角线上的第4个数13为标准,(14+15+16)-(12+11+10)=(14-10)+(15-11)+(16-12)=3×4,
以对角线上的第5个数21为标准,(17+18+19+20)-(22+23+24+25)=(17-22)+(18-23)+(19-24)+(20-25)=-4×5,
…,
以对角线上的第45个数1981为标准,(1937+1938+…+1980)-(1982+1983+…+2025)=(1937-1982)+(1938-1983)+…+(1980-2025)=-44×45,
所以S1-S2=1×2-2×3+3×4-4×5+…+43×44-44×45
=2(1-3)+4×(3-5)+…+44×(43-45)
=-4-8-…-88
=-(4+8+12+…+88)
=-
| 1 |
| 2 |
| 44 |
| 2 |
=-
| 1 |
| 2 |
=-1012.
故答案为:-1012.
点评:本题是对数字变化规律的考查,根据对角线上的数字,所在的列向上的数字减去所在的行向左的数字,分别求出差值并以此得到规律是解题的关键.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
 (2012•南浔区二模)如图,点A(a,b)是抛物线
(2012•南浔区二模)如图,点A(a,b)是抛物线 +(-1)2009+(π-2).
+(-1)2009+(π-2). +(-1)2009+(π-2).
+(-1)2009+(π-2).