题目内容
 如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,点A、B、C表示某旅游景区三个缆车站的位置,线段AB、BC表示连接缆车站的钢缆,已知A、B、C三点在同一铅直平面内,它们的海拔高度AA′,BB′,CC′分别为110米、310米、710米,钢缆AB的坡度i1=1:2,钢缆BC的坡度i2=1:1,景区因改造缆车线路,需要从A到C直线架设一条钢缆,那么钢缆AC的长度是多少米?(注:坡度i是指坡面的铅直高度与水平宽度的比)考点:解直角三角形的应用-坡度坡角问题
专题:几何图形问题
分析:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,分别求出AE、CE,利用勾股定理求解AC即可.
解答:解:过点A作AE⊥CC′于点E,交BB′于点F,过点B作BD⊥CC′于点D,
则△AFB、△BDC、△AEC都是直角三角形,四边形AA′B′F,BB′C′D和BFED都是矩形,
∴BF=BB′-B′F=BB′-AA′=310-110=200,
CD=CC′-C′D=CC′-BB′=710-310=400,
∵i1=1:2,i2=1:1,
∴AF=2BF=400,BD=CD=400,
又∵EF=BD=400,DE=BF=200,
∴AE=AF+EF=800,CE=CD+DE=600,
∴在Rt△AEC中,AC=
=
=1000(米).
答:钢缆AC的长度是1000米.

则△AFB、△BDC、△AEC都是直角三角形,四边形AA′B′F,BB′C′D和BFED都是矩形,
∴BF=BB′-B′F=BB′-AA′=310-110=200,
CD=CC′-C′D=CC′-BB′=710-310=400,
∵i1=1:2,i2=1:1,
∴AF=2BF=400,BD=CD=400,
又∵EF=BD=400,DE=BF=200,
∴AE=AF+EF=800,CE=CD+DE=600,
∴在Rt△AEC中,AC=
| AE2+CE2 |
| 8002+6002 |
答:钢缆AC的长度是1000米.
点评:本题考查了解直角三角形的应用,解答本题的关键是理解坡度坡角的定义,及勾股定理的表达式,难度一般.

练习册系列答案
相关题目
截止2013年10月余额宝规模达到2 175000 000元,用科学记数法表示捐款数应为( )
| A、2.175×1010元 |
| B、2.175×109元 |
| C、21.75×108元 |
| D、217.5×107元 |
 如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,且∠BAC=32°.
如图,AB为⊙O的直径,PA、PC是⊙O的切线,A、C为切点,且∠BAC=32°.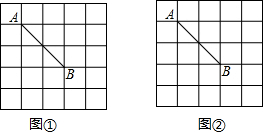 如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.一条线段AB的两端点落在格点(即小正方形的顶点)上,且长度为2
如图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.一条线段AB的两端点落在格点(即小正方形的顶点)上,且长度为2