题目内容
20.解方程:(1)x-3=x(x-3)(用分解因式法)
(2)x2+8x+9=0(用配方法)
(3)3x2-7x-6=0(用公式法)
分析 (1)直接提取公因式(x-3),利用因式分解法解方程即可;
(2)首先移项进行配方,进而开方求出方程的解;
(3)首先找出方程中a,b和c的值,求出b2-4ac的值,代入公式即可求解.
解答 解:(1)∵x-3=x(x-3),
∴(x-3)(x-1)=0,
∴x-1=0或x-3=0,
∴x1=1,x2=3;
(2)∵x2+8x+9=0,
∴x2+8x+16=7,
∴(x+4)2=7,
∴x+4=±$\sqrt{7}$,
∴x1=-4+$\sqrt{7}$,x2=-4-$\sqrt{7}$;
(3)∵3x2-7x-6=0,
∴a=3,b=-7,c=-6,
∴b2-4ac=121,
∴x=$\frac{7±\sqrt{121}}{2×3}$,
∴x1=3,x2=-$\frac{2}{3}$.
点评 本题考查了一元二次方程的解法.解一元二次方程常用的方法有直接开平方法,配方法,公式法,因式分解法,要根据方程的特点灵活选用合适的方法.

练习册系列答案
相关题目
9.阅读下列材料:如果(x+1)2-9=0,那么(x+1)2-32=(x+1+3)(x+1-3)=(x+4)(x-2),则(x+4)(x-2)=0,由此可知:x1=-4,x2=2.根据以上材料计算x2-2x-1=0的根为( )
| A. | x1=1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | B. | x1=-1+$\sqrt{2}$,x2=11-$\sqrt{2}$ | C. | x1=-1+$\sqrt{2}$,x2=1-$\sqrt{2}$ | D. | x1=1+$\sqrt{2}$,x2=-1-$\sqrt{2}$ |
10.下列命题错误的是( )
| A. | 两个相似三角形的对应角相等,对应值成比例 | |
| B. | 两个全等三角形一定相似 | |
| C. | 两个等腰三角形一定是相似 | |
| D. | 相似的两个三角形不一定全等 |
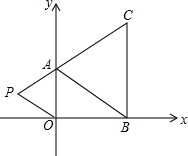 如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式,|a+b-5|+$\sqrt{2a-b-1}$=0,(c-4)2≤0.
如图,在直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式,|a+b-5|+$\sqrt{2a-b-1}$=0,(c-4)2≤0.
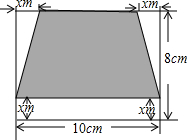 茗茗家有一块长10m,宽8m的矩形空地,妈妈准备在该空地上建造一个花园,并使花园的面积为整个矩形面积的$\frac{3}{5}$,茗茗设计的一种方案如图所示,请你帮茗茗求出图中x的值.
茗茗家有一块长10m,宽8m的矩形空地,妈妈准备在该空地上建造一个花园,并使花园的面积为整个矩形面积的$\frac{3}{5}$,茗茗设计的一种方案如图所示,请你帮茗茗求出图中x的值.