题目内容
 如图,直线AB和CD相交于O,OE⊥AB,那么图中∠DOE与∠COA的关系是( )
如图,直线AB和CD相交于O,OE⊥AB,那么图中∠DOE与∠COA的关系是( )| A、对顶角 | B、相等 | C、互余 | D、互补 |
考点:垂线,余角和补角,对顶角、邻补角
专题:计算题
分析:先由垂直的定义得到∠AOE=∠BOE=90°,则∠DOE+∠BOD=90°,再根据对顶角相等得到∠BOD=∠AOC,所以∠DOE+∠AOC=90°,然后根据互余的定义进行判断.
解答:解:∵OE⊥AB,
∴∠AOE=∠BOE=90°,
∴∠DOE+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠DOE+∠AOC=90°,
即∠DOE与∠COA互余.
故选C.
∴∠AOE=∠BOE=90°,
∴∠DOE+∠BOD=90°,
∵∠BOD=∠AOC,
∴∠DOE+∠AOC=90°,
即∠DOE与∠COA互余.
故选C.
点评:本题考查了垂线:当两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足.垂线的性质过一点有且只有一条直线与已知直线垂直.也考查了对顶角和两角互余.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
不等式5(x+2)≤28-2x的非负整数解有( )个.
| A、1 | B、2 | C、3 | D、无数个 |
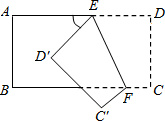 如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )
如图所示,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置.若∠AED′=50°,则∠DEF等于( )| A、50° | B、65° |
| C、75° | D、60° |
若方程组
的解x与y的和是2,则a的值为( )
|
| A、-4 | B、4 | C、0 | D、任意数 |
使式子
有意义的实数x的取值范围是( )
| 2x+3 |
A、x>
| ||
B、x>
| ||
C、x≥-
| ||
D、x≥-
|
下列方程中不一定是一元二次方程的是( )
| A、(a-3)x2=8 (a≠3) | ||||
| B、ax2+bx+c=0 | ||||
| C、(x+3)(x-2)=x+5 | ||||
D、
|