题目内容
如图,抛物线y=| 4 | 57 |
(1)求线段AB与线段CD的长;
(2)求△APQ的面积S与t的函数关系式;
(3)连接BE.是否存在这样的时刻t,使得∠AEB=∠BDC?
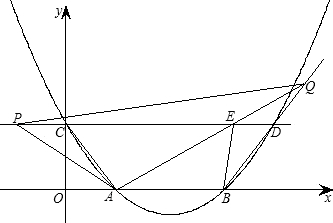 若存在请求出t的值;若不存在,请说明理由.
若存在请求出t的值;若不存在,请说明理由.
分析:(1)先令y=0,求出A,B,两点的坐标,再令x=0,求出C点坐标,即可求出C,D两点的坐标,再用两点间的距离公式求出AB,CD两点间的距离即可.
(2)作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,由(1)中所求A,B,C,D,的坐标,根据三角形相似可求出PF,QG,FG,的长,再利用梯形的面积减去△APF与△BQG的面积即可.
(3)若∠AEB=∠BDC,则根据△AEC∽△EBD,△QED∽△QAB求出t的值.
(2)作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,由(1)中所求A,B,C,D,的坐标,根据三角形相似可求出PF,QG,FG,的长,再利用梯形的面积减去△APF与△BQG的面积即可.
(3)若∠AEB=∠BDC,则根据△AEC∽△EBD,△QED∽△QAB求出t的值.
解答:解:(1)当y=0时,
(x-6)(x-19)=0,
∴x1=6,x2=19,
∴x1=6,x2=19,
∴A(6,0),B(19,0),
∴AB=13.
当x=0时,y=8,
∴C(0,8).
当y=8时,
(x-6)(x-19)=8,
解得x1=0,x2=25,
∴D(25,8),
∴CD=25.
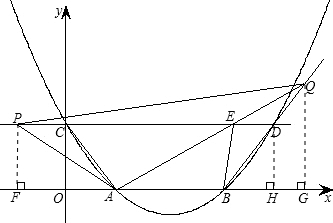
(2)如图,
作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,
∵CD∥x轴,
∴PF=DH=OC=8,OH=CD=25,
∵OA=6,OB=19,
∴BH=OH-OB=6,
∴BD=
=10,
∵△BDH∽△BQG,
∴
=
=
.
由题意得CP=DQ=t,AF=t+6,
∴
=
=
,
∴QG=
t+8,BG=
t+6,
∴FG=t+19+
t+6=
t+25.
∴S=S梯形PFGQ-S△PAF-S△AQG=
(PF+QG)•FG-
AF•PF-
AG•QG=
t2+8.8t+100.
(3)∵AC=BD=10,
∴四边形ABDC为等腰梯形,
∴∠ACD=∠BDC.
若∠AEB=∠BDC,则∠AEC+∠BED=∠BED+∠EBD,
∴∠AEC=∠EBD.
同理,∠BED=∠EAC.
∴△AEC∽△EBD.
∴
=
,
即
=
,
∴DE=5(DE=20>AB=13舍去),
∵△QED∽△QAB,
∴
=
,
即
=
,
解得t=
.
| 4 |
| 57 |
∴x1=6,x2=19,
∴x1=6,x2=19,
∴A(6,0),B(19,0),
∴AB=13.
当x=0时,y=8,
∴C(0,8).
当y=8时,
| 4 |
| 57 |
解得x1=0,x2=25,
∴D(25,8),
∴CD=25.

(2)如图,
作PF⊥x轴于F,QG⊥x轴于G,DH⊥x轴于H,
∵CD∥x轴,
∴PF=DH=OC=8,OH=CD=25,
∵OA=6,OB=19,
∴BH=OH-OB=6,
∴BD=
| BH2+DH2 |
∵△BDH∽△BQG,
∴
| BD |
| BQ |
| DH |
| QG |
| BH |
| BG |
由题意得CP=DQ=t,AF=t+6,
∴
| 10 |
| 10+t |
| 8 |
| QG |
| 6 |
| BG |
∴QG=
| 4 |
| 5 |
| 3 |
| 5 |
∴FG=t+19+
| 3 |
| 5 |
| 8 |
| 5 |
∴S=S梯形PFGQ-S△PAF-S△AQG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 5 |
(3)∵AC=BD=10,
∴四边形ABDC为等腰梯形,
∴∠ACD=∠BDC.
若∠AEB=∠BDC,则∠AEC+∠BED=∠BED+∠EBD,
∴∠AEC=∠EBD.
同理,∠BED=∠EAC.
∴△AEC∽△EBD.
∴
| AC |
| DE |
| CE |
| BD |
即
| 10 |
| DE |
| 25-DE |
| 10 |
∴DE=5(DE=20>AB=13舍去),
∵△QED∽△QAB,
∴
| ED |
| AB |
| QD |
| QB |
即
| 5 |
| 13 |
| t |
| t+10 |
解得t=
| 25 |
| 4 |
点评:本题比较复杂,综合考查了二次函数图象上点的坐标特点及等腰梯形的性质,注意某个图形无法解答时,常常放到其他图形中,利用图形间的“和差“关系求解.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
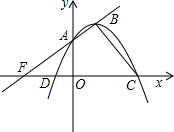 点D,C,点C在x轴正方向.
点D,C,点C在x轴正方向.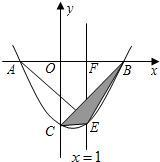 坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度.
坐标为(-2,0);直线x=1与抛物线交于点E,与x轴交于点F,且45°≤∠FAE≤60度. (2012•温州模拟)如图,抛物线
(2012•温州模拟)如图,抛物线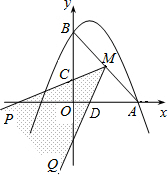 已知抛物线y=
已知抛物线y=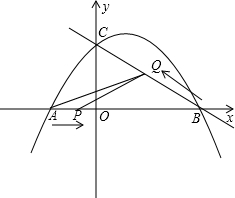 角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.