题目内容
如图,抛物线y=ax2+(a+c)x+c的顶点B在第一象限,它与y轴正半轴交于点A,与x轴交于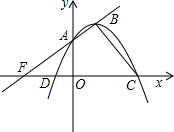 点D,C,点C在x轴正方向.
点D,C,点C在x轴正方向.(1)求点D的坐标;
(2)若直线AB和x轴负方向交于点F,∠BFC=45°,比较DF:DO和tan∠BCF的大小.
分析:(1)令y=0,解关于x的一元二次方程ax2+(a+c)x+c=0,再根据点D在x轴的负半轴即可得解;
(2)根据∠BFC=45°可得△AOF是等腰直角三角形,根据点D与点A的坐标分别表示出DF与DO的长度,即可求出其比值,利用顶点公式写出点B的坐标,过点B作BE⊥x轴于点E,根据∠BFC=45°可知△BEF是等腰直角三角形,利用BE=EF列式求出a、c的关系,再根据BE与CE的长度列式求出tan∠BCF,然后进行比较即可得解.
(2)根据∠BFC=45°可得△AOF是等腰直角三角形,根据点D与点A的坐标分别表示出DF与DO的长度,即可求出其比值,利用顶点公式写出点B的坐标,过点B作BE⊥x轴于点E,根据∠BFC=45°可知△BEF是等腰直角三角形,利用BE=EF列式求出a、c的关系,再根据BE与CE的长度列式求出tan∠BCF,然后进行比较即可得解.
解答: 解:(1)y=0时,ax2+(a+c)x+c=0,
解:(1)y=0时,ax2+(a+c)x+c=0,
△=b2-4ac=(a+c)2-4ac=(a-c)2,
结合图形可知,a<0,c>0,
∴x=
=
=
,
解得x1=-1,x2=-
,
∴点D的坐标是(-1,0);
(2)当x=0时,y=ax2+(a+c)x+c=c,
∵∠BFC=45°,
∴△AOF是等腰直角三角形,
∴OF=c,
∴DF=OF-DO=c-1,
∴DF:DO=(c-1):1=c-1,
∵-
=-
,
=
=-
,
∴顶点B的坐标是(-
,-
),
过点B作BE⊥x轴,垂足为E,则△BEF是等腰直角三角形,
∴BE=EF,
即-
=-
+c,
整理得a+c=2,
又∵CE=CO-OE=-
-(-
)=
,
∴tan∠BCF=
=
=
=
=c-1,
∴DF:DO=tan∠BCF=c-1.
 解:(1)y=0时,ax2+(a+c)x+c=0,
解:(1)y=0时,ax2+(a+c)x+c=0,△=b2-4ac=(a+c)2-4ac=(a-c)2,
结合图形可知,a<0,c>0,
∴x=
-b±
| ||
| 2a |
-(a+c)±
| ||
| 2a |
| -(a+c)±(c-a) |
| 2a |
解得x1=-1,x2=-
| c |
| a |
∴点D的坐标是(-1,0);
(2)当x=0时,y=ax2+(a+c)x+c=c,
∵∠BFC=45°,
∴△AOF是等腰直角三角形,
∴OF=c,
∴DF=OF-DO=c-1,
∴DF:DO=(c-1):1=c-1,
∵-
| b |
| 2a |
| a+c |
| 2a |
| 4ac-b2 |
| 4a |
| 4ac-(a+c)2 |
| 4a |
| (a-c)2 |
| 4a |
∴顶点B的坐标是(-
| a+c |
| 2a |
| (a-c)2 |
| 4a |
过点B作BE⊥x轴,垂足为E,则△BEF是等腰直角三角形,
∴BE=EF,
即-
| (a-c)2 |
| 4a |
| a+c |
| 2a |
整理得a+c=2,
又∵CE=CO-OE=-
| c |
| a |
| a+c |
| 2a |
| a-c |
| 2a |
∴tan∠BCF=
| BE |
| CE |
-
| ||
|
| c-a |
| 2 |
| c-(2-c) |
| 2 |
∴DF:DO=tan∠BCF=c-1.
点评:本题是对二次函数的综合考查,包括二次函数解析式与x轴的交点的求解,等腰直角三角形的性质,顶点坐标的求解,以及正切函数的求解,综合性较强,难度较大,但只要认真分析,仔细计算也不难求解.

练习册系列答案
相关题目
 两点,试问当x为何值时,线段CD有最大值,其最大值为多少?
两点,试问当x为何值时,线段CD有最大值,其最大值为多少? O为坐标原点,抛物线上一点C的横坐标为1.
O为坐标原点,抛物线上一点C的横坐标为1. 此抛物线上,矩形面积为12,
此抛物线上,矩形面积为12, 与x轴交于点A、B,点A的坐标为(-2,0).
与x轴交于点A、B,点A的坐标为(-2,0).