Question

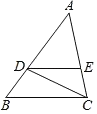
【题目】如图，在△ABC中，点D，E分别在AB，AC边上，DE∥BC，AD＝2BD，BC＝6．

（1）求DE的长；

（2）连接CD，若∠ACD＝∠B，求CD的长．

Answer 1

【答案】（1）DE＝4，（2）CD＝2．

【解析】

（1）设AD＝2x，BD＝x，易证△ADE∽△ABC，利用相似三角形的性质可求出DE的长度；

（2）证明△ADE∽△ACD，利用相似三角形的性质即可求出得出，从而可求出CD的长度．

解：设AD＝2x，BD＝x，

∴AB＝3x，

∵DE∥BC，

∴△ADE∽△ABC，

∴＝，

∴，

∴DE＝4，

（2）∵∠ACD＝∠B，

∠ADE＝∠B，

∴∠ADE＝∠ACD，

∵∠A＝∠A，

∴△ADE∽△ACD，

∴，

设AE＝2y，AC＝3y，

∴，

∴AD＝y，

∴，

∴CD＝2．