Question

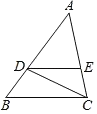
【题目】 如图，等边△ABC中，点D是BC上任一点，以AD为边作∠ADE=∠ADF=60°,分别交AC,AB于点E,F.

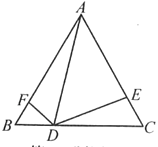
(1)求证：AD2=AEAC.

(2)已知BC=2,设BD的长为x,AF的长为y.

①求y关于x的函数表达式；

②若四边形AFDE外接圆直径为,求x的值

Answer 1

【答案】（1）见解析（2）① ②

【解析】

（1）根据等边三角形的性质，可求得∠BAC=∠ACD=∠ABC=60°，然后根据相似三角形的判定得到△ADE∽△ACD，再根据相似三角形的对应边成比例得证；

（2）①根据BC=2，BD=x，AF=y，可得DC=2-x，然后根据相似三角形的判定得到△ACD∽△DBF，再根据相似三角形的对应边成比例得到x、y的关系式；

②由已知可得A、F、D、E四点共圆，从而求得EF=，再进一步根据相似三角形的判定与性质，由△ABD∽△DCE得到CE的结果，进而判断出△AEF是等边三角形，得到AF=EF，从而求解.

（1）△ABC为等边三角形

∴∠BAC=∠ACD=∠ABC=60°

在△ADE和△ADC中

∴△ADE∽△ACD

∴

∴AD=AC.AE

（2）①已知BC=2，BD=x，AF=y，则DC=2-x

在△ACD和△BFD中

∴△ACD∽△DBF

∴

∴

∴y= （0＜x＜2）

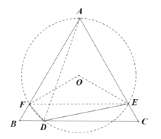
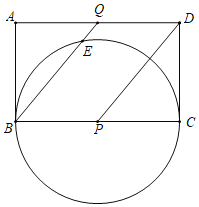
②由已知可得A、F、D、E四点共圆，如图所示，

∠BAC=60°，∠FDE=120°，∠FOE=120°

⊙O的直径为

∴EF=

在△ABD和△DCE中

∴△ABD∽△DCE

∴

∴

∴CE=-x+x，AE=2-CE=

∵y=

∴AF=AE

AEF为等边三角形，AF=EF=

∴y==

∴