题目内容
(本小题满分12分)如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,开口向下的抛物线经过点A,B,且其顶点P在⊙C上.

(1)求∠ACB的大小;
(2)写出A,B两点的坐标;
(3)试确定此抛物线的解析式;
(4)在该抛物线上是否存在一点D,使线段OP与CD互相平分?若存在,求出点D的坐标;若不存在,请说明理由.
(1)120°;(2)A(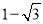 ,0),B(
,0),B(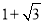 ,0);(3)
,0);(3)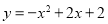 ;(4)D(0,2).
;(4)D(0,2).
【解析】
试题分析:(1)可通过构建直角三角形来求解.过C作CH⊥AB于H,在直角三角形ACH中,根据半径及C点的坐标即可用三角形函数求出∠ACB的值.
(2)根据垂径定理可得出AH=BH,然后在直角三角形ACH中可求出AH的长,再根据C点的坐标即可得出A、B两点的坐标.
(3)根据抛物线和圆的对称性,即可得出圆心C和P点必在抛物线的对称轴上,因此可得出P点的坐标为(1,3).然后可用顶点式二次函数通式来设抛物线的解析式.根据A或B的坐标即可确定抛物线的解析式.
(4)如果OP、CD互相平分,那么四边形OCPD是平行四边形.因此PC平行且相等于OD,那么D点在y轴上,且坐标为(0,2).然后将D点坐标代入抛物线的解析式中即可判定出是否存在这样的点.
试题解析:(1)作CH⊥x轴,H为垂足,
∵CH=1,半径CB=2,∠BCH=60°,∴∠ACB=120°.
(2)∵CH=1,半径CB=2,∴HB=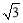 ,故A(
,故A(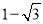 ,0),B(
,0),B(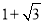 ,0).
,0).
(3)由圆与抛物线的对称性可知抛物线的顶点P的坐标为(1,3)
设抛物线解析式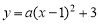 ,把点B(
,把点B(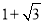 ,0)代入上式,解得
,0)代入上式,解得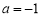 ,∴
,∴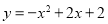 ;
;
(4)假设存在点D使线段OP与CD互相平分,则四边形OCPD是平行四边形,∴PC∥OD且PC=OD.
∵PC∥y轴,∴点D在y轴上.
又∵PC=2,∴OD=2,即D(0,2).
又D(0,2)满足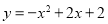 ,∴点D在抛物线上,∴存在D(0,2)使线段OP与CD互相平分.
,∴点D在抛物线上,∴存在D(0,2)使线段OP与CD互相平分.
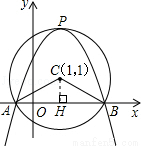
考点:二次函数综合题.


 (0º<
(0º<
 B.
B. C.
C. D.
D.
 的图象在
的图象在 轴上方的一部分,对于这段图象与
轴上方的一部分,对于这段图象与 轴所围成的阴影部分的面积,你认为与其最接近的值是( )
轴所围成的阴影部分的面积,你认为与其最接近的值是( )
 C.
C. D.32
D.32