题目内容
15.在平面直角坐标系中,直线y=2x+4交y轴与点A,交x轴于点B,点C在x轴的正半轴上,且△ABC的面积为12.(1)如图1,求直线AC的解析式;
(2)如图2,若CE⊥AB,垂足为点E,交y轴于点D,求线段AD的长;
(3)在(2)的条件下,将△ADE及直线AC均水平向右平移m个单位得到△A′D′E′及直线A′C′,点P在直线A′C′上,且P点的横坐标为$\frac{30}{11}$,当PD′+PE′的值最小时,求m的值及这个最小值.
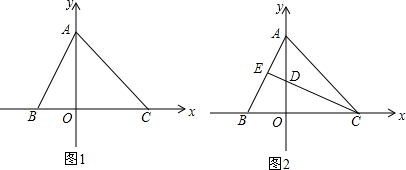
分析 (1)先求的A、B两点的坐标,然后根据△ABC的面积为12可求得BC的长,从而得到点C的坐标,最后利用待定系数法求得AC的解析式即可;
(2)证明∠DCO=∠BAO,然后根据$\frac{OD}{OC}=\frac{OB}{OA}$可求得OD的长,从而得到AD的长;
(3)作点D关于AC的对称点F,连接EF交AC于点G,过点E作EH⊥AD,垂足为H.首先求得点E的坐标,然后求得直线EF的解析式,接下来求得EF与AC的交点F的坐标,最后根据平移的性质可求得m的值,由平移的性质可知PD′+PE′的最小值等于EF的长.
解答 解:(1)令直线y=2x+4的y=0得:2x+4=0,解得x=-2.
∴点B的坐标为(-2,0).
令直线y=2x+4的x=0得y=4,
∴点A的坐标为(0,4).
∵△ABC的面积为12,
∴$\frac{1}{2}BC•OA=12$,即$\frac{1}{2}×4×BC=12$.
解得:BC=6.
所以点C的坐标为(4,0).
设直线AC的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{4k+b=0}\\{b=4}\end{array}\right.$.
解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$,
∴直线AC的解析式为y=-x+4.
(2)∵CE⊥AB,
∴∠AED=90°.
∴∠AED=∠DOC=90°.
∵∠ADE=∠ODC
∴∠BAO=∠BCE.
∴$\frac{OD}{OC}=\frac{OB}{OA}=\frac{1}{2}$.
∴OD=2.
∴AD=2.
(3)作点D关于AC的对称点F,连接EF交AC于点G,过点E作EH⊥AD,垂足为H.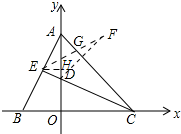
∵点D关于AC的对称点F,
∴点F的坐标为(2,4).
∵tan∠EAD=$\frac{1}{2}$,
∴$\frac{ED}{AD}=\frac{1}{\sqrt{5}}$.
∴$\frac{ED}{2}=\frac{1}{\sqrt{5}}$.
∴ED=$\frac{2\sqrt{5}}{5}$.
在Rt△EHD中,EH=$\frac{2\sqrt{5}}{5}$ED=$\frac{4}{5}$.HD=$\frac{\sqrt{5}}{5}ED$$\frac{\sqrt{5}}{5}×\frac{2\sqrt{5}}{5}=\frac{2}{5}$.
∴点E的坐标为(-0.8,2.4).
设直线EF的解析式为y=ax+b.
∴$\left\{\begin{array}{l}{-0.8a+b=2.4}\\{2a+b=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{4}{7}}\\{b=\frac{20}{7}}\end{array}\right.$.
∴直线EF的解析式为y=$\frac{4}{7}x+\frac{20}{7}$.
将y=$\frac{4}{7}x+\frac{20}{7}$与y=-x+4联立,解得x=$\frac{8}{11}$.
设平移的距离为m个单位,
∴$\frac{8}{11}+m$=$\frac{30}{11}$.
解得:m=2.
由平移的性质可知:PD′+PE′=EF=$\sqrt{[2-(-0.8)^{2}+(4-2.4)^{2}}$=4$\sqrt{65}$.
答:m=2,PD′+PE′的最小值为4$\sqrt{65}$.
点评 本题主要考查的是一次函数的综合应用、轴对称路径最短问题、平移的性质求得平以前EF与AC的交点的坐标是解题的关键.

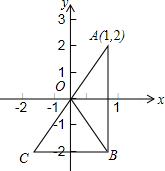 如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )
如图,x轴是△AOB的对称轴,y轴是△BOC的对称轴,点A的坐标为(1,2),则点C的坐标为( )| A. | (-1,-2) | B. | (1,-2) | C. | (-1,2) | D. | (-2,-1) |
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )| A. | 美 | B. | 丽 | C. | 江 | D. | 西 |
| A. | 有两个不相等的正根 | B. | 有两个不相等的负根 | ||
| C. | 没有实数根 | D. | 有两个相等的实数根 |
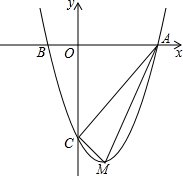 如图,已知二次函数的图象与x轴的交点横坐标为方程x2-4x-12=0的两根,与y轴交于点C(0,-8).
如图,已知二次函数的图象与x轴的交点横坐标为方程x2-4x-12=0的两根,与y轴交于点C(0,-8). 细心观察右图,认真分析下列各式,然后回答问题:
细心观察右图,认真分析下列各式,然后回答问题: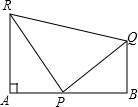 如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度.
如图,RA⊥AB,QB⊥AB,P是AB上的一点,RP=PQ=a,RA=h,QB=k,∠RPA=75°,∠QPB=45°,求AB的长度. 如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点A的坐标是(3,$\sqrt{3}$).
如图,在平面直角坐标系中,矩形OABC的对角线AC平行于x轴,边OA与x轴正半轴的夹角为30°,OC=2,则点A的坐标是(3,$\sqrt{3}$).