题目内容
2.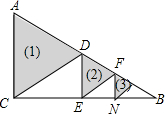 如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB上中线CD,得到第1个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第2个三角形DEF;依次作下去…则第1个三角形的面积等于$\frac{\sqrt{3}}{4}$a2,第n个三角形的面积等于$\frac{\sqrt{3}{a}^{2}}{{2}^{2n}}$.
如图,在△ABC中,∠ACB=90°,∠A=60°,AC=a,作斜边AB上中线CD,得到第1个三角形ACD;DE⊥BC于点E,作Rt△BDE斜边DB上中线EF,得到第2个三角形DEF;依次作下去…则第1个三角形的面积等于$\frac{\sqrt{3}}{4}$a2,第n个三角形的面积等于$\frac{\sqrt{3}{a}^{2}}{{2}^{2n}}$.
分析 根据直角三角形斜边上的中线等于斜边的一半可得CD=AD,然后判定出△ACD是等边三角形,同理可得被分成的第二个、第三个…第n个三角形都是等边三角形,再根据后一个等边三角形的边长是前一个等边三角形的边长的一半求出第n个三角形的边长,然后根据等边三角形的面积公式求解即可.
解答 解:∵∠ACB=90°,CD是斜边AB上的中线,
∴CD=AD,
∵∠A=60°,
∴△ACD是等边三角形,
同理可得,被分成的第二个、第三个…第n个三角形都是等边三角形,
∵CD是AB的中线,EF是DB的中线,…,
∴第一个等边三角形的边长CD=DB=$\frac{1}{2}$AB=AC=a,
∴第一个三角形的面积为$\frac{\sqrt{3}}{4}$a2,
第二个等边三角形的边长EF=$\frac{1}{2}$DB=$\frac{1}{2}$a,
…
第n个等边三角形的边长为$\frac{1}{{2}^{n-1}}$a,
所以,第n个三角形的面积=$\frac{1}{2}$×$\frac{1}{{2}^{n-1}}$a×($\frac{\sqrt{3}}{2}$•$\frac{1}{{2}^{n-1}}$a)=$\frac{\sqrt{3}{a}^{2}}{{2}^{2n}}$.
故答案为$\frac{\sqrt{3}}{4}$a2,$\frac{\sqrt{3}{a}^{2}}{{2}^{2n}}$.
点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质,等边三角形的判定与性质,三角形的面积判断出后一个三角形的边长是前一个三角形边长的一半,求出第n个等边三角形的边长是解题的关键.

练习册系列答案
相关题目
13.解方程2x-5=3x-9时,移项正确的是( )
| A. | 2x+3x=9+5 | B. | 2x-3x=9+5 | C. | 2x-3x=-9+5 | D. | 2x-3x=9-5 |
10.现有下列叙述:
①若a<b,则3a-5<3b-5;
②若-2a<10,则a>-5;
③若x+5<8,则x<3;
④若3a>-9,则a<-$\frac{1}{3}$.
其中正确的有( )
①若a<b,则3a-5<3b-5;
②若-2a<10,则a>-5;
③若x+5<8,则x<3;
④若3a>-9,则a<-$\frac{1}{3}$.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.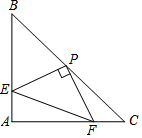 如图:已知△ABC,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC与E,F,给出以下五个结论:①EF=CP;②CF=AE;③2PF2=EF2;④∠AEP+∠AFP=180°;⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=$\frac{1}{2}$S△ABC.上述结论中始终正确的有( )
如图:已知△ABC,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC与E,F,给出以下五个结论:①EF=CP;②CF=AE;③2PF2=EF2;④∠AEP+∠AFP=180°;⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=$\frac{1}{2}$S△ABC.上述结论中始终正确的有( )
 如图:已知△ABC,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC与E,F,给出以下五个结论:①EF=CP;②CF=AE;③2PF2=EF2;④∠AEP+∠AFP=180°;⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=$\frac{1}{2}$S△ABC.上述结论中始终正确的有( )
如图:已知△ABC,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC与E,F,给出以下五个结论:①EF=CP;②CF=AE;③2PF2=EF2;④∠AEP+∠AFP=180°;⑤当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合),S四边形AEPF=$\frac{1}{2}$S△ABC.上述结论中始终正确的有( )| A. | ①②③④⑤ | B. | ①②⑤ | C. | ①③④⑤ | D. | ②③④⑤ |
7.下列各数中,最小的数是( )
| A. | 0 | B. | 3 | C. | -2016 | D. | -0.001 |
14.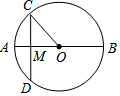 如图,AB是⊙O的直径,弦CD⊥AB于点M,AM=2,BM=8,则CD的长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点M,AM=2,BM=8,则CD的长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点M,AM=2,BM=8,则CD的长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点M,AM=2,BM=8,则CD的长为( )| A. | 4 | B. | 5 | C. | 8 | D. | 16 |
11.欢欢发烧了,妈妈带她去看医生,结果测量出体温是39.2℃,用了退烧药后,以每15分钟下降0.2℃的速度退烧,则两小时后,欢欢的体温是( )℃.
| A. | 38.2 | B. | 37.2 | C. | 38.6 | D. | 37.6 |
12.已知am=3,an=4,则am+n=( )
| A. | 12 | B. | 7 | C. | 6 | D. | 8 |
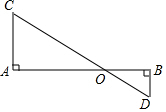 如图,已知AC⊥AB,BD⊥AB,AO=5cm,BO=3cm,OC=10cm.求OD和CD.
如图,已知AC⊥AB,BD⊥AB,AO=5cm,BO=3cm,OC=10cm.求OD和CD.