Question

【题目】[问题解答]

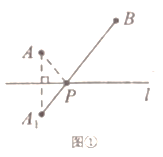
两个城镇与一条公路位置如图①所示.现电信部门需在公路上修建一座信号发射塔要求发射塔到两个城镇与的距离之和最短．

　　　　　　

解：点作关于直线的对称点连结,

与直线的交点即为所求的点.

点关于直线对称，

直线垂直平分

点即为所求的点。(两点之间线段最短)

请根据以上问题解答，完成下列问题．

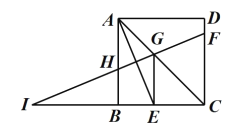
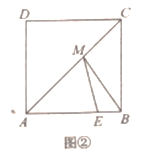
[方法运用]如图②，在正方形中，点在边上，点在对角线AC上，

（1）当点是边的中点时，则的最小值为 ；

（2）若求周长的最小值．

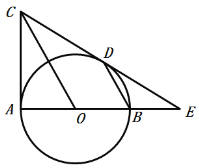
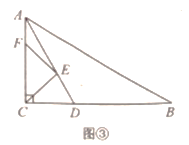
[拓展提升]如图③，在中，，AD平分交于点，点分别在上，则的最小值为 ．

Answer 1

【答案】[方法运用]（1）；（2）△BEM周长的最小值6；[拓展提升]．

【解析】

[方法运用]

（1）易知B关于AC的对称点D，连接DE交AC于M，则的最小值为DE，根据勾股定理即可求出DE长；

（2）作点E作关于AC的对称点E1，连结BE1，交AC与点M，求出的最小值，即可求出三角形周长的最小值；

[拓展提升]

由角平分线可得到F点对称点始终在AB上，延长CE交AB于P点，则CP=，当CP⊥AB时，即可求得最小值．

解：[方法运用]

（1）易知B点关于AC对称点为D点，连接DE交AC于M，

的最小值为，

∴则的最小值为．

（2）作点E作关于AC的对称点E1，连结BE1，交AC与点M．

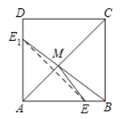
∵点E、E1关于AC对称，

∴AC垂直平分EE1

∴，

∴，

∴，

又∵BE=4-3=1，

∴△BEM周长的最小值6．

[拓展提升]

∵AD平分，

∴F点关于AD的对称点始终在AB上，

延长CE交AB于P点，则P点为F点的对称点，即CP=，

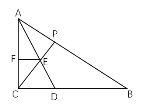
∴当CP⊥AB时，有最小值，

∵，

∴AB=5，

∴CP=，

∴的最小值为．