题目内容
6. 在△ABC中,DB=CE,DE的延长线交BC的延长线于P,求证:AD•BP=AE•CP.
在△ABC中,DB=CE,DE的延长线交BC的延长线于P,求证:AD•BP=AE•CP.
分析 过点C作CG∥DP交AB于G,根据平行线分线段成比例定理可得$\frac{AD}{DG}=\frac{AE}{AC}$,$\frac{BD}{DG}=\frac{BP}{CP}$,变形比例式表示DG,得$\frac{AD•EC}{AE}$=$\frac{BD•CP}{BP}$,又BD=EC,得到$\frac{AD}{AE}=\frac{CP}{BP}$,化为等积式即可.
解答 解:过点C作CG∥DP交AB于G,
∴$\frac{AD}{DG}=\frac{AE}{AC}$,$\frac{BD}{DG}=\frac{BP}{CP}$,
∴DG=$\frac{AD•EC}{AE}$,DG=$\frac{BD•CP}{BP}$,
∴$\frac{AD•EC}{AE}$=$\frac{BD•CP}{BP}$,
∵BD=EC,
∴$\frac{AD}{AE}=\frac{CP}{BP}$,
∴AD•BP=AE•CP.
点评 本题考查了平行线分线段成比例定理以及比例式变形,解决此题的关键是由平行构造比例式.

练习册系列答案
相关题目
17.做重复试验:抛掷同一枚啤酒瓶盖1000次.经过统计得“凸面向上”的次数约为420次,则可以由此估计抛掷这枚啤酒瓶盖出现“凹面向上”的概率约为( )
| A. | 0.22 | B. | 0.42 | C. | 0.50 | D. | 0.58 |
11.若一间教室的面积为80~120m2,104m2相当于n间教室的面积,则n最接近( )
| A. | 10 | B. | 100 | C. | 1000 | D. | 10000 |
15.若$\frac{3xy}{2x+3y}$中的x和y都扩大到原来的2倍,那么分式的值( )
| A. | 缩小为原来的一半 | B. | 不变 | ||
| C. | 扩大到原来的2倍 | D. | 扩大到原来的4倍 |
 如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了1000米.
如图,某登山运动员从营地A沿坡角为30°的斜坡AB到达山顶B,如果AB=2000米,则他实际上升了1000米.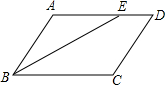 如图,平行四边形ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,平行四边形ABCD的周长20.
如图,平行四边形ABCD中,∠ABC的平分线交边AD于E,DC=4,DE=2,平行四边形ABCD的周长20.