题目内容
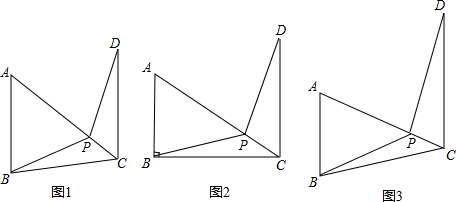
6.已知△ABC和△BDE中,∠ABC=∠CDE=90°,CB=CD,连结BD、AE交于点F.(1)如图1,若∠CAB=∠CED,探究AF与EF之间的数量关系;
(2)如图2,若∠CAB=∠ECD=α,求$\frac{AF}{FE}$的值(用含α的式子表示).
分析 (1)过A作AH⊥CD与H,交BD于G,由∠CDE=∠ABC=90°,于是得到AG∥ED,根据平行线的性质得到∠FED=∠FAG,∠FDE=∠FGA,根据等腰三角形的性质得到∠CDB=∠CBD,由余角的性质得到∠BGA=∠DGH=∠ABD,求得△ABG是等腰三角形,得到AB=AG,推出△ABC≌△CDE,根据全等三角形的性质得到AB=DE,等量代换得到AG=DE,证得△EFD≌△AGF,即可得到结论;
(2)根据△FAG∽△FDE,于是得到$\frac{AF}{EF}=\frac{ED}{AG}$,等量代换得到$\frac{AF}{EF}=\frac{AB}{AG}$,根据三角函数的定义对对对AB=$\frac{CB}{tanα}$,ED=$\frac{CD}{tanα}$,于是得到结论.
解答 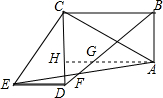 解:(1)过A作AH⊥CD与H,交BD于G,
解:(1)过A作AH⊥CD与H,交BD于G,
∵∠CDE=∠ABC=90°,
∴AG∥ED,
∴∠FED=∠FAG,∠FDE=∠FGA,
∵CB=CD,
∴∠CDB=∠CBD,
∴∠DGH+∠CDB=90°,
∵∠ABD+∠CBD=90°,
∴∠BGA=∠DGH=∠ABD,
∴△ABG是等腰三角形,
∴AB=AG,
在△ABC与△CDE中,
$\left\{\begin{array}{l}{∠ABC=∠CDE}\\{∠BAC=∠DCE}\\{BC=CD}\end{array}\right.$,
∴△ABC≌△CDE,
∴AB=DE,
∴AG=DE,
在△DEF与△AGF中,
$\left\{\begin{array}{l}{∠FED=∠GAF}\\{∠EFC=∠AFG}\\{EF=AG}\end{array}\right.$,
∴△EFD≌△AGF,
∴EF=AF;
(2)∵∠FED=∠FAG,∠FDE=∠FGA,
∴△FAG∽△FDE,
∴$\frac{AF}{EF}=\frac{ED}{AG}$,
∴$\frac{AF}{EF}=\frac{AB}{AG}$,
∵∠CAB=∠ECD=α,
∴AB=$\frac{CB}{tanα}$,ED=$\frac{CD}{tanα}$,
∴$\frac{AF}{EF}$=$\frac{1}{ta{n}^{2}α}$.
点评 本题考查了全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.

| A. | .3或-4 | B. | .-3或4 | C. | 4 | D. | 3 |
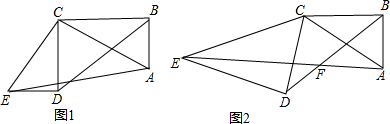
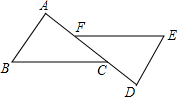 如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )
如图,AB∥DE,AF=DC,若要证明△ABC≌△DEF,还需补充的条件是( )| A. | AC=DF | B. | AB=DE | C. | ∠A=∠D | D. | BC=EF |
| A. | -$\frac{5}{3}$ | B. | 2π | C. | $\sqrt{0.01}$ | D. | $\root{3}{-27}$ |
| A. | 没有实数根 | B. | 只有一个实数根 | ||
| C. | 有两个不相等的实数根 | D. | 有两个相等的实数根 |
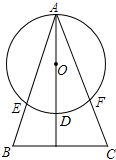 AD是⊙O的直径,AD⊥BC,AB、AC分别与圆相交于E,F,求证:AB•AE=AF•AC.
AD是⊙O的直径,AD⊥BC,AB、AC分别与圆相交于E,F,求证:AB•AE=AF•AC.