题目内容
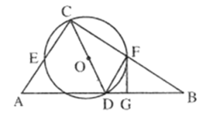
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,连接
,连接![]() ,以
,以![]() 为直径作
为直径作![]() ,分别与
,分别与![]() ,
,![]() 交于点
交于点![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() ,交
,交![]() 于点
于点![]() ,则
,则![]() 的长为____________.
的长为____________.
【答案】![]()
【解析】
先F是BC中点求出BF=CF=4,进而求出CD=BD=5,再由勾股定理求出DF=3,再判断出FG⊥BD,利用面积即可得出结论.
如图,连接OF
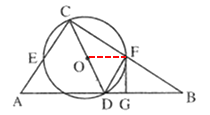
∵点F是BC中点,
∴CF=BF=![]() BC=4,
BC=4,
∵CD是⊙O的直径,
∴∠CFD=90°,
∴CD=BD=5,
∴DF=![]() =3,∠OCF=∠B,
=3,∠OCF=∠B,
∵OC=OF,
∴∠OCF=∠OFC
∴∠OFC=∠B,
∵点F是BC中点,点O是CD中点,
∴OF∥AB,
∴∠OFD=∠GDF,
∵FG是⊙O的切线,
∴∠OFG=90°,
∴∠OFD+∠DFG=90°,
∴∠FDG+∠GDF=90°,
∴∠FDG=90°
∴FG⊥AB,
∴S△BDF=![]() DF×BF=
DF×BF=![]() BD×FG,
BD×FG,
∴FG=![]() ,
,
故答案为![]() .
.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目