Question

【题目】在平面直角坐标系中xOy中，抛物线y＝x2﹣4x+m+2的顶点在x轴上．

（1）求抛物线的表达式；

（2）点Q是x轴上一点，

①若在抛物线上存在点P，使得∠POQ＝45°，求点P的坐标．

②抛物线与直线y＝1交于点E，F（点E在点F的左侧），将此抛物线在点E，F（包含点E和点F）之间的部分沿x轴向左平移n个单位后得到的图象记为G，若在图象G上存在点P，使得∠POQ＝45°，求n的取值范围．

Answer 1

【答案】（1）y＝x2﹣4x+4；（2）①点P的坐标为（1，1）或（4，4）；②在图象G上存在点P，使得∠POQ＝45°，n的取值范围为0≤n≤4．

【解析】

（1）根据抛物线顶点在x轴上，列式计算可得m的值；

（2）由∠POQ＝45°，作直线y＝x，交抛物线y＝x2﹣4x+4于点P，联立解析式求出P点坐标即可；

（3）分两种情况考虑：当点P，Q在y轴右侧时与点P，Q在y轴左侧时，列出不等式求解即可.

解：（1）∵抛物线y＝x2﹣4x+m+2的顶点在x轴上，

∴＝0，

解得：m＝2，

∴抛物线的表达式为y＝x2﹣4x+4．

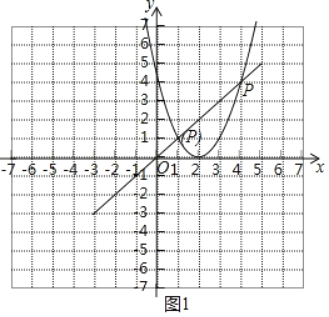
（2）①作直线y＝x，交抛物线y＝x2﹣4x+4于点P，如图1所示．

联立直线OP及抛物线的表达式成方程组，得：，

解得：，，

∴点P的坐标为（1，1）或（4，4）．

②当y＝1时，x2﹣4x+4＝1，

解得：x1＝1，x2＝3，

∴点E的坐标为（1，1），点F的坐标为（3，1）．

分两种情况考虑：

（i）当点P，Q在y轴右侧时，∵抛物线y＝x2﹣4x+4与直线y＝x交于点（1，1），

∴当1≤3﹣n≤3时，图象G上存在点P，使得∠POQ＝45°，解得：0≤n≤2；

（ii）当点P，Q在y轴左侧时，同①可得出，抛物线y＝x2﹣4x+4与直线y＝﹣x交于点（﹣1，﹣1）或（﹣4，﹣4），

∴当﹣1≤3﹣n≤1时，图象G上存在点P，使得∠POQ＝45°，解得：2≤n≤4．

综上所述：若在图象G上存在点P，使得∠POQ＝45°，n的取值范围为0≤n≤4．