题目内容
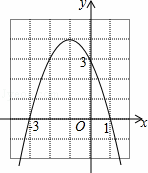
已知关于x的一元二次方程mx2﹣(m+2)x+2=0.
(1)证明:不论m为何值时,方程总有实数根;
(2)m为何整数时,方程有两个不相等的正整数根.
解:(1)△=(m+2)2﹣8m
=m2﹣4m+4
=(m﹣2)2,
∵不论m为何值时,(m﹣2)2≥0,
∴△≥0,
∴方程总有实数根;
(2)解方程得,x= ,
,
x1= ,x2=1,
,x2=1,
∵方程有两个不相等的正整数根,
∴m=1或2,m=2不合题意,
∴m=1.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
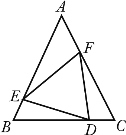
如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC∽△AED的是( )

|
| A. | ∠AED=∠B | B. | ∠ADE=∠C | C. |
| D. |
|
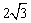 ,则菱形ACEF的面积为 .
,则菱形ACEF的面积为 .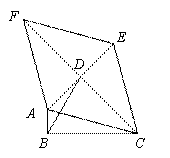
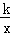 与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.
与新函数的图象交于点C(1,a),点D是线段AC上一动点(不包括端点),过点D作x轴的平行线,与新函数图象交于另一点E,与双曲线交于点P.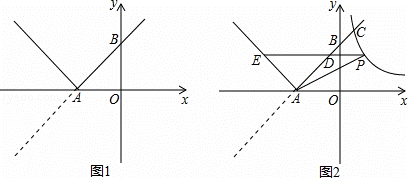
 =
=
 =
=
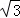 ﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据:
﹣1)米,现要在E、F之间修一条笔直道路,求这条道路EF的长(结果取整数,参考数据: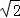 =1.41,
=1.41,