��Ŀ����
��ͼ1����ֱ֪��y=x+3��x�ύ�ڵ�A����y�ύ�ڵ�B����ֱ����x���·��IJ�����x�ᷭ�ۣ��õ�һ���º�����ͼ��ͼ�еġ�V�����ߡ�����
��1������о�����ͼ��ķ��������о��º������������ʣ������º����Ľ���ʽ��
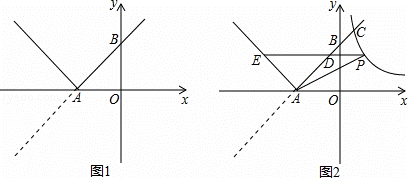
��2����ͼ2��˫����y=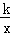 ���º�����ͼ���ڵ�C��1��a������D���߶�AC��һ���㣨�������˵㣩������D��x���ƽ���ߣ����º���ͼ������һ��E����˫���߽��ڵ�P��
���º�����ͼ���ڵ�C��1��a������D���߶�AC��һ���㣨�������˵㣩������D��x���ƽ���ߣ����º���ͼ������һ��E����˫���߽��ڵ�P��
�������PAD����������ֵ��
��̽�����ڵ�D�˶��Ĺ����У��ı���PAEC�ܷ�Ϊƽ���ı��Σ����ܣ������ʱ��D�����ꣻ�����ܣ���˵�����ɣ�
�⣺��1����ͼ1�������������º������������ʣ��ٺ�������СֵΪ0��
�ں���ͼ��ĶԳ���Ϊֱ��x=﹣3��
�������A������Ϊ��﹣3��0���������������
��x��﹣3ʱ����Ȼy=x+3��
�ڵ�x��﹣3ʱ���������ʽΪy=kx+b��
��ֱ��y=x+3�У���x=﹣4ʱ��y=﹣1��
��㣨﹣4��﹣1������x��ĶԳƵ�Ϊ��﹣4��1����
�ѣ�﹣4��1������﹣3��0������y=kx+b��
�� �����
����� ��
��
��y=﹣x﹣3��
�����������º����Ľ���ʽΪy= ��
��
��2����ͼ2���١ߵ�C��1��a����ֱ��y=x+3�ϣ�
��a=1+3=4��
�ߵ�C��1��4����˫����y= �ϣ�
�ϣ�
��k=1��4=4��y= ��
��
�ߵ�D���߶�AC��һ���㣨�������˵㣩��
������D������Ϊ��m��m+3������﹣3��m��1��
��DP��x�ᣬ�ҵ�P��˫�����ϣ�
��P�� ��m+3����
��m+3����
��PD= ﹣m��
﹣m��
���PAD�����Ϊ
S= ��
�� ﹣m������m+3��=﹣
﹣m������m+3��=﹣ m2﹣
m2﹣ m+2=﹣
m+2=﹣ ��m+
��m+ ��2+
��2+ ��
��
��a=﹣ ��0��
��0��
�൱m=﹣ ʱ��S�����ֵ��Ϊ
ʱ��S�����ֵ��Ϊ ��
��
�֡�﹣3��﹣ ��1��
��1��
���PAD����������ֵΪ ��
��
���ڵ�D�˶��Ĺ����У��ı���PAEC����Ϊƽ���ı��Σ��������£�
����DΪAC���е�ʱ��������Ϊ��﹣1��2������ʱP�������Ϊ��2��2����E�������Ϊ��﹣5��2����
��DP=3��DE=4��
��EP��AC���ܻ���ƽ�֣�
���ı���PAEC����Ϊƽ���ı��Σ�


 ͬ������ϵ�д�
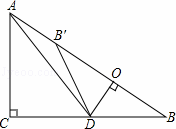
ͬ������ϵ�д���ͼ����ABC�У�AB=5��AC=6��BC=4����AB�Ĵ�ֱƽ���߽�AC�ڵ�D�����BDC���ܳ��ǣ�������

| �� | A�� | 8 | B�� | 9 | C�� | 10 | D�� | 11 |
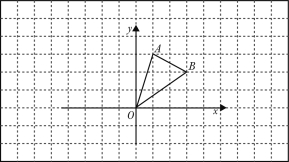
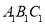 ���뻭����
���뻭���� ��
��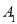 �������Ϊ ��
�������Ϊ �� (2)�����������ٴε�������ǰȥ��Ԯ�����������ٲ��䣬�����ڵ�E�����ϣ����ECD������ֵ�� (�ο����ݣ�
(2)�����������ٴε�������ǰȥ��Ԯ�����������ٲ��䣬�����ڵ�E�����ϣ����ECD������ֵ�� (�ο����ݣ� ��
�� ��
�� )
)