题目内容
(本题10分)如图,△ABC中,AB=AC,D、E、F分别在BC、AB、AC上,且BE=CD,BD=CF.
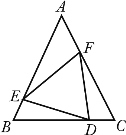
(1)求证:DE=DF;
(2)当∠A的度数为多少时,△DEF是等边三角形,并说明理由.
(1)证明详见解析;(2)∠A=60°.
【解析】
试题分析:(1)通过证明△BDE和 △CFD全等得到DE=DF;
(2)利用三角形全等的性质及等式的性质证得∠EDF=∠C,当∠A=60°时,∠B=∠C =60°,此时∠EDF=∠C=60°,所以△DEF是等边三角形.
试题解析:证明:(1)∵AB=AC,
∴ ∠B=∠C,
在△BDE和 △CFD 中,
 ,
,
∴ △BDE≌ △CFD(SAS).
∴DE=DF;
(2)当∠A=60°时, △DEF是等边三角形.
理由:∵ △BDE≌ △CFD,
∴∠BDE=∠CFD,
∵∠BDE+∠EDF=∠CFD+∠C,
∴∠EDF=∠C,
又∵DE=DF,要使△DEF是等边三角形,只要∠EDF=60°,
则∠C=∠EDF=60°,
∴当∠A=60°时,∠B=∠C =60°,此时△DEF是等边三角形.
考点:全等三角形的判定和性质;等边三角形的判定.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
 为线段
为线段 上一点,
上一点, ,
, ,
, .求证:
.求证: .
.
 ∥
∥ ,∠1=3∠2,∠2=25°,求
,∠1=3∠2,∠2=25°,求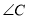 的度数.
的度数.
 B.
B.
 D.
D.
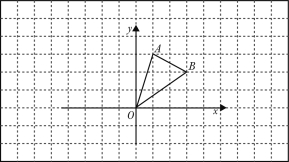
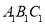 ,请画出△
,请画出△ ;
;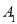 点的坐标为 .
点的坐标为 . 的图象向上平移
的图象向上平移 个单位,所得图象的函数表达式为 .
个单位,所得图象的函数表达式为 .