Question

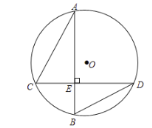
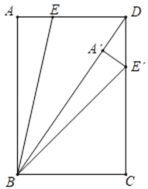
【题目】如图，在矩形ABCD中，AB＝8，BC＝6，E为AD上一点，将△BAE绕点B顺时针旋转得到△BA′E′，当点A′，E′分别落在BD，CD上时，则DE的长为_____．

Answer 1

【答案】

【解析】

根据勾股定理可求BD=10，由旋转的性质可得AE=A'E，AB=A'B=8，∠BA'E'=90°，由△BCD∽△E'A'D，可得，可得A'E'=AE=，即可求DE的长．

∵四边形ABCD是矩形

∴∠DAB＝∠C＝90°，AD＝BC＝6，AB＝CD＝8，

∴BD＝＝10，

∵将△BAE绕点B顺时针旋转得到△BA′E′，

∴AE＝A'E，AB＝A'B＝8，∠BA'E'＝90°

∴A'D＝BD﹣BA'＝2，

∵∠BDC＝∠BDC，∠DA'E'＝∠C＝90°，

∴△BCD∽△E'A'D

∴

即

∴A'E'＝＝AE

∴DE＝AD﹣AE＝

故答案为