Question

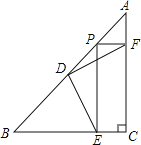
【题目】已知，菱形ABCD中，E，F分别是对角线BD和边BC上一点，且满足∠EAF=∠ABD=．

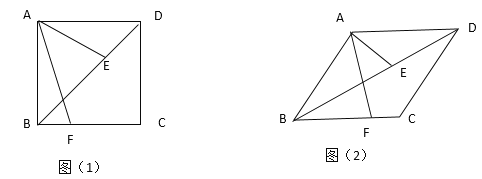
（1）如图（1），当=45°时，求证：AF=AE

（2）如图（2），探究AF与AE的数量关系（用含的锐角三角函数表示）

Answer 1

【答案】（1）见解析；（2）AF=2AEcos

【解析】

（1）连接AC，证明△AFC∽△AED，由相似三角形的性质，即可得到答案；

（2）设AF与BE交于点G，作EH⊥AF于H，由菱形的性质，以及相似三角形的判定和性质，得到AE=EF，由三角函数即可得到答案．

解：（1）连结AC，

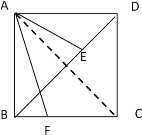
当=45°时，

∴∠EAF=∠ABD=45°，

∴四边形ABCD正方形，

∴∠ACF=∠ADE=∠DAC=45°，

∴∠EAF=∠DAC=45°，

∴∠CAF=∠DAE，

∴△AFC∽△AED ，

∴

∴；

（2）设AF与BE交于点G，

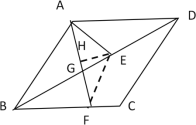
∵∠EAF=∠ABD=

又菱形ABCD

∴∠EAF=∠ABD=∠FBG=

∵∠BGF=∠AGE

∴△AGE∽△BGF

∴，

∵∠BGA=∠FGE

∴△AGB∽△EGF

∴∠EFG=∠ABG=

∴AE=EF

作EH⊥AF于H

∵，

∴AH=AEcos

∴ AF=2AEcos；