Question

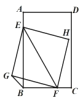
【题目】如图，△ABC是等腰直角三角形，∠C=90°，点D是AB的中点，点P是AB上的一个动点（点P与点A、B不重合），矩形PECF的顶点E，F分别在BC，AC上．

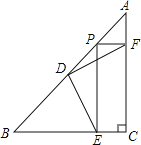
（1）探究DE与DF的关系，并给出证明；

（2）当点P满足什么条件时，线段EF的长最短？说明理由．

Answer 1

【答案】（1）DE=DF，DE⊥DF，证明见解析；（2）点P与点D重合时，线段EF最短，证明见解析

【解析】

（1）连接CD，首先根据△ABC是等腰直角三角形，∠C=90°，点D是AB的中点得到CD=AD，CD⊥AD，然后根据四边形PECF是矩形得到△APF是等腰直角三角形，从而得到△DCE≌△DAF，证得DE=DF，DE⊥DF；
（2）根据DE=DF，DE⊥DF，得到EF=DE=DF，从而得到当DE和DF同时最短时，EF最短得到此时点P与点D重合线段EF最短．

（1）DE=DF，DE⊥DF，

证明：连接CD，

∵△ABC是等腰直角三角形，∠C=90°，点D是AB的中点，

∴CD=AD，CD⊥AD，∠DCE=45°，

∴∠CDA=90°，

∵四边形PECF是矩形，

∴CE=FP，FP∥CB，

∴△APF是等腰直角三角形，

∴AF=PF=EC，

∴∠A=∠DCE=45°，

∴△DCE≌△DAF（SAS），

∴DE=DF，∠ADF=∠CDE，

∵∠EDF=∠EDC+∠CDF=∠CDF+∠ADF=90°，

∴DE⊥DF；

（2）∵DE=DF，DE⊥DF，

∴EF=DE=DF，

∴当DE和DF同时最短时，EF最短，

∴当DF⊥AC，DE⊥AB时，二者最短，

∴此时点P与点D重合，

∴点P与点D重合时，线段EF最短．