题目内容
 如图,已知AB∥CD,∠ABE=60°,∠D=50°,则∠E=
如图,已知AB∥CD,∠ABE=60°,∠D=50°,则∠E=考点:平行线的性质,三角形的外角性质
专题:
分析:根据平行线的性质得出∠EFC=∠ABE=60°,根据三角形外角性质得出∠E+∠D=∠EFC=60°,把∠D=50°代入求出即可.
解答:解:∵AB∥CD,
∴∠EFC=∠ABE=60°,
∵∠E+∠D=∠EFC,
∴∠E=∠EFC-∠D=60°-50°=10°;
∴∠EFC=∠ABE=60°,
∵∠E+∠D=∠EFC,
∴∠E=∠EFC-∠D=60°-50°=10°;
点评:本题考查了平行线的性质以及三角形外角性质的应用,关键是得出∠E+∠D=∠EFC=60°;

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
(x-y)与(y-x)的乘积是( )
| A、x2-y2 |
| B、y2-x2 |
| C、-x2-y2 |
| D、-x2+2xy-y2 |
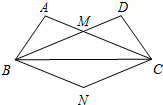 如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.
如图,在△ABC和△DCB中,AC=BD,AB=CD,AC、BD交于点M.