��Ŀ����
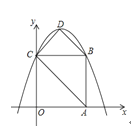
����Ŀ�� ��ͼ��![]() �У�
��![]() ������
������![]() ��
��![]() ��������ÿ��
��������ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() ��
��![]() ��
��![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ��ƽ���ߣ������
��ƽ���ߣ������![]() ����
����![]() ��ֱ��ֱ�߽��ڵ�
��ֱ��ֱ�߽��ڵ�![]() �����
�����![]() ���˶�ʱ��Ϊ
���˶�ʱ��Ϊ![]() (��)
(��)![]()

��1���ú�![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��2����![]() ����
����![]() ����ʱt��ֵ��
����ʱt��ֵ��
��3����![]() ��
��![]() �غϲ���ͼ�ε����Ϊ
�غϲ���ͼ�ε����Ϊ![]() (ƽ����λ)����
(ƽ����λ)����![]() ���
���![]() ������ϵʽ��
������ϵʽ��
��4������![]() ������
������![]() ����������ij�߷��ۣ�����ǰ��������������γ����Σ�ֱ��д����ʱ
����������ij�߷��ۣ�����ǰ��������������γ����Σ�ֱ��д����ʱ![]() ��ֵ.
��ֵ.
���𰸡���1��![]() ����2��
����2��![]() ����3��
����3��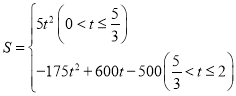 ����4��
����4��![]() ��
��![]() ��
��![]() .
.
��������
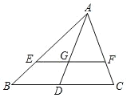
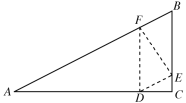
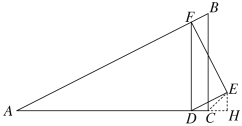
��1��������ɵ�DF��AC��EF��AB��DE��AB��Ȼ������ͬ�ǵ������ȿɵá�DFE=��A������֤����ADF�ס�FED���Ƴ�![]() ��Ȼ�������ADF�ס�ACB���ɷֱ��ú�t��ʽ�ӱ�ʾ��DF��AF��Ȼ��ɵ�DE��
��Ȼ�������ADF�ס�ACB���ɷֱ��ú�t��ʽ�ӱ�ʾ��DF��AF��Ȼ��ɵ�DE��
��2������![]() ����
����![]() ����ʱ������ADF�ס�DCE���г�����ʽ���DC=2t��Ȼ�����AC=20�з������t���ɣ�
����ʱ������ADF�ס�DCE���г�����ʽ���DC=2t��Ȼ�����AC=20�з������t���ɣ�
��3����![]() ʱ��
ʱ��![]() �����������������ʽ��⼴�ɣ���
�����������������ʽ��⼴�ɣ���![]() ʱ��
ʱ��![]() ����EH��AC��AC���ӳ����ڵ�H��EF��BC��N��DE��BC��M������ƽ���߷��߶γɱ����������NM���������������ʽ��⼴�ɣ�
����EH��AC��AC���ӳ����ڵ�H��EF��BC��N��DE��BC��M������ƽ���߷��߶γɱ����������NM���������������ʽ��⼴�ɣ�
��4����������������ij�߷��ۣ�����ǰ��������������γ����Σ���֪��ʱ![]() Ϊ���������Σ�Ȼ���������ۣ��ٵ�DE=CEʱ���ڵ�DC=CEʱ���۵�DE=DCʱ���ֱ��г�������t��ֵ����.
Ϊ���������Σ�Ȼ���������ۣ��ٵ�DE=CEʱ���ڵ�DC=CEʱ���۵�DE=DCʱ���ֱ��г�������t��ֵ����.
�⣺��1���������֪��DF��AC��EF��AB��DE��AB��
���ADF=90������EFA=90����
���DEF=90������DFA+��DFE =90����
�ߡ�DFA+��A =90����
���DFE=��A��
�ߡ�DEF=��ADF=90����
����ADF�ס�FED��
��![]() ��
��
�ߡ�C��90����
����ADF�ס�ACB��
��AC=20��BC=10��
��AB=![]() ��
��
��![]() ��
��![]() ��
��
�֡�AD=10t��
��DF=5t��AF=![]() ��
��
��![]() ��
��
��DE=![]() ��
��
��2������![]() ����
����![]() ����ʱ��
����ʱ��
��DE��AB��
����ADF�ס�DCE��
��![]() ��
��
�ɣ�1����֪��DE=![]() ��AF=
��AF=![]() ��AD=10t��
��AD=10t��
��DC=2t��
��10t+2t=20��
��ã�![]() ��
��
��3����DE=![]() ��
��
��EF=2DE=![]() ��
��
�൱![]() ʱ��
ʱ��![]() ��
��
��D����C��ʱ��t=20��10��2��
�൱![]() ʱ��
ʱ��![]() ��
��
��ͼ����EH��AC��AC���ӳ����ڵ�H��EF��BC��N��DE��BC��M��
ͬ��2���ɵ�DH=2t��
��CH=10t+2t-20=12t-20��DC=20-10t��
��BC��DF��
��![]() ��
��
��BC��EH��
��![]() ��
��
��![]() ����
����![]() ��
��
��![]() ��
��
��![]() ��
��
����������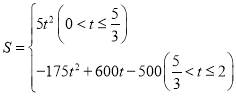 ��
��
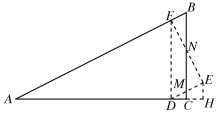
��4����������������ij�߷��ۣ�����ǰ��������������γ����Σ���֪��ʱ![]() Ϊ���������Σ�
����������
�ٵ�DE=CEʱ����ͼ����EH��DC�ڵ�H��
�ɣ�3���ɵ�DH=2t��
��DC=4t��
��10t+4t=20��
��ã�![]() ��
��
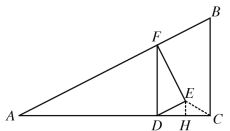
�ڵ�DC=CEʱ����ͼ����EH��AC��AC���ӳ����ڵ�H������CE��
�ɣ�3����֪��DE=![]() ��DH=2t��CH=12t-20��DC=20-10t��
��DH=2t��CH=12t-20��DC=20-10t��
��EH=t��
�ɹ��ɶ����ã�(12t-20)2+t2=(20-10t)2��
��ã�![]() ��
��
�۵�DE=DCʱ��
��DE=![]() ��DC=20-10t��
��DC=20-10t��
��![]() ��
��
��ã�![]() ��
��
������������![]() ��
��![]() ��
��![]() ʱ����
ʱ����![]() ����������ij�߷��ۣ�����ǰ��������������γ�����.
����������ij�߷��ۣ�����ǰ��������������γ�����.

����Ŀ����ͼ�Ǽס�����������˶�Ա��10��������Գɼ�������ͳ��ͼ.
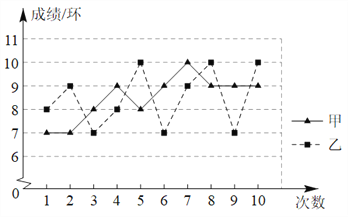
��1����������ͼ�����б���������
�˶�Ա | ƽ���� | ��λ�� | ���� |
�� | 8.5 | 9 | |
�� | 8.5 |
��2����������ͼ��������ѧͳ��֪ʶ�Լס��������˶�Ա�����ˮƽ�������۲�˵������.