题目内容
 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )
如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为( )A、
| ||
B、5
| ||
| C、13cm | ||
D、
|
考点:平面展开-最短路径问题
专题:
分析:要求长方体中两点之间的最短路径,最直接的作法,就是将长方体展开,然后利用两点之间线段最短解答.
解答: 解:如图所示:
解:如图所示:
∵长方体的底面边长分别为2cm和4cm,高为5cm.
∴PA=4+2+4+2=12(cm),QA=5cm,
∴PQ=
=13cm.
故选C.
 解:如图所示:
解:如图所示:∵长方体的底面边长分别为2cm和4cm,高为5cm.
∴PA=4+2+4+2=12(cm),QA=5cm,
∴PQ=
| PA2+AQ2 |
故选C.
点评:本题的是平面展开-最短路径问题,解答此类问题时要先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.

练习册系列答案
相关题目
 如图,P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,若AE=4,则AF=( )
如图,P是∠BAC的平分线AD上一点,PE⊥AB于E,PF⊥AC于F,若AE=4,则AF=( )| A、1 | B、2 | C、4 | D、8 |
某服装店新开张,第一天销售服装a件,第二天的销售件数是第一天销售件数的3倍还多10件,则第二天销售了( )
| A、(a+10)件 |
| B、(3a+13)件 |
| C、(10a+3)件 |
| D、(3a+10)件 |

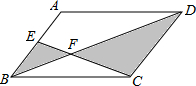 如图,在?ABCD中,E为AB的中点,CE、BD相交于点F.设?ABCD的面积为4,求图中阴影部分的面积.
如图,在?ABCD中,E为AB的中点,CE、BD相交于点F.设?ABCD的面积为4,求图中阴影部分的面积.