题目内容
6.计算化简(1)10$\sqrt{\frac{1}{5}}$+$\frac{5}{2}$$\sqrt{\frac{4}{5}}$-$\sqrt{45}$
(2)$\sqrt{18}$÷($\frac{1}{\sqrt{3}}$-$\frac{1}{\sqrt{6}}$)
(3)(2x3y)2•(-2xy)+(-2x3y)3÷(2x2)
(4)($\frac{1}{x-2}$-1)÷$\frac{x-3}{{x}^{2}-4}$•$\frac{x}{{x}^{2}+4x+4}$.
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先把括号内通分,再把除法运算化为乘法运算,然后分母有理化后进行二次根式的乘法运算即可;
(3)先利用同底数幂的乘除法则运算,然后合并即可;
(4)先把括号内通分,再把除法运算化为乘法运算,然后约分即可.
解答 解:(1)原式=2$\sqrt{5}$+$\sqrt{5}$-3$\sqrt{5}$
=0;
(2)原式=3$\sqrt{2}$÷$\frac{\sqrt{2}-1}{\sqrt{6}}$
=3$\sqrt{2}$•$\frac{\sqrt{6}}{\sqrt{2}-1}$
=6$\sqrt{3}$($\sqrt{2}$+1)
=6$\sqrt{6}$+6$\sqrt{3}$;
(3)原式=4x6y2•(-2xy)-8x9y3÷(2x2)
=-8x7y3-4x7y3
=-12x7y3;
(4)原式=$\frac{1-x+2}{x-2}$•$\frac{(x+2)(x-2)}{x-3}$•$\frac{x}{(x+2)^{2}}$
=-$\frac{x}{x+2}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.

练习册系列答案
相关题目
14.下列方程中是关于x的一元二次方程的是( )
| A. | x2+2x=x2-1 | B. | x3+2x2+3=0 | C. | x(x-1)=1 | D. | 3x2-2xy-5y2=0 |
1. 如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )
 如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )
如图,数轴上A、B两点分别对应实数a、b,则下列结论错误的是( )| A. | a+b<0 | B. | a2>b2 | C. | ab<0 | D. | |a|<|b| |
16.至2010年10月30日上海世博会累计入园人数约7277.99万人,这个数据精确到( )
| A. | 百分位 | B. | 百位 | C. | 千位 | D. | 万位 |
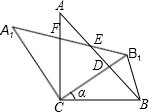 如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.
如图,△ABC中,∠ACB=90°,AC=BC=1,将△ABC绕点C逆时针旋转得到△A1B1C,旋转角为ɑ(0°<ɑ<90°),连接BB1.设CB1交AB于点D,A1B1分别交AB、AC于点E,F.