题目内容
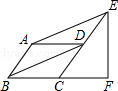
如图,▱ABCD中,对角线AC与BD相交于点E,∠AEB=45°,BD=2,将△ABC沿AC所在直线翻折180°到其原来所在的同一平面内,若点B的落点记为B′,则DB′的长为 ![]() .
.

考点:平行四边形的性质;等腰直角三角形;翻折变换(折叠问题).
分析:如图,连接BB′.根据折叠的性质知△BB′E是等腰直角三角形,则BB′=![]() BE.又B′E是BD的中垂线,则DB′=BB′.
BE.又B′E是BD的中垂线,则DB′=BB′.
解答:解:∵四边形ABCD是平行四边形,BD=2,
∴BE=![]() BD=1.
BD=1.
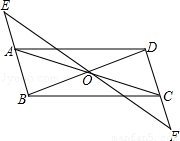
如图2,连接BB′.
根据折叠的性质知,∠AEB=∠AEB′=45°,BE=B′E.
∴∠BEB′=90°,
∴△BB′E是等腰直角三角形,则BB′=![]() BE=
BE=![]() .
.
又∵BE=DE,B′E⊥BD,
∴DB′=BB′=![]() .
.
故答案是:![]() .
.

点评:本题考查了平行四边形的性质,等腰三角形的判定与性质以及翻折变换(折叠的性质).推知DB′=BB′是解题的关键.

练习册系列答案
相关题目

 .
.
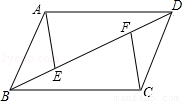
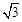 ,则AB的长是
.
,则AB的长是
.