题目内容
16.如果直线y=kx+b经过一、二、四象限,则k,b的取值分别是( )| A. | k>0,b>0 | B. | k>0,b<0 | C. | k<0,b>0 | D. | k<0,b<0 |
分析 根据一次函数y=kx+b图象在坐标平面内的位置关系先确定k,b的取值范围,从而求解.
解答 解:由一次函数y=kx+b的图象经过第一、二、四象限,
又由k<0时,直线必经过二、四象限,故知k<0.
再由图象过一、二象限,即直线与y轴正半轴相交,所以b>0.
故选:C.
点评 本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限;k<0时,直线必经过二、四象限;b>0时,直线与y轴正半轴相交;b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
7.在一个不透明的袋子中,有3个白球和2个红球,它们只有颜色上的区别,从袋子中随机地摸出1个球,摸到白球的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{6}$ |
4.已知a是一元二次方程x2-3x-5=0的较小的根,则下面对a的估计正确的是( )
| A. | -2<a<-1 | B. | 2<a<3 | C. | -3<a<-4 | D. | 4<a<5 |
11. 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )
 实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )
实数a,b在数轴上的对应点如图所示,则|a-b|-$\sqrt{{a}^{2}}$的结果为( )| A. | b | B. | 2a-b | C. | -b | D. | b-2a |
1.若$\frac{a}{b}$=$\frac{5}{3}$,则$\frac{b}{a-b}$的值等于( )
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
8.据中新社北京2010年12月8日电,2010年中国粮食总产量达到0.000 000 005 464吨,用科学记数法表示为( )吨.
| A. | 5.464×10-7 | B. | 5.464×10-8 | C. | 5.464×10-9 | D. | 5.464×10-10 |
5.下列说法:①全等图形的形状相同、大小相等;②三边对应相等的两个三角形全等;③全等三角形的对应角相等;④全等三角形的周长、面积分别相等,其中正确的说法为( )
| A. | ①②④ | B. | ①③④ | C. | ②③④ | D. | ①②③④ |
6.下列运算中,正确的是( )
| A. | a3•a2=a6 | B. | (ab)2=a2b2 | C. | 2(a-1)=2a-1 | D. | (a+b)2=a2+b2 |
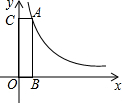 如图,过反比例函数y=$\frac{4}{x}$(x>0)上一点A作AB⊥x轴于点B,AC⊥y轴于点C,则四边形OBAC的面积是( )
如图,过反比例函数y=$\frac{4}{x}$(x>0)上一点A作AB⊥x轴于点B,AC⊥y轴于点C,则四边形OBAC的面积是( )