Question

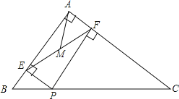
【题目】如图：已知．

（1）读句画图：画的角平分线、交、于点、，且、交于点，过点作交的延长线于．

（2）在（1）的条件下解决下面问题：

①填表

的度数
的度数	__________	______________	______________

②根据图中的数据，你发现无论是什么角，总是__________（填锐角、钝角或直角）．

③若过点作于，你能猜想与之间的数量关系吗？说明理由．（在（1）中的图上作于）

Answer 1

【答案】（1）见解析；（2）①；②锐角；③，理由见解析

【解析】

（1）根据要求画出图形即可；

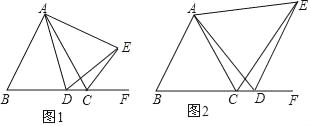
（2）①当∠ACB=40°时，根据角平分线定义及三角形外角的性质求出∠AIF，然后可得∠BFC，同理求出其他两种情况；

②根据∠BFC=∠AIF=90°-∠ACB，得出∠BFC＜90°，即可判断；

③利用直角三角形两锐角互余可得，结合可得答案．

解：（1）如图所示；

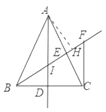
（2）①∵AD，BE是△ABC的角平分线，

∴∠BAI=∠BAC，∠ABI=∠ABC，

∴∠AIF=∠ABI+∠ABI=（∠BAC+∠ABC）=（180°-∠ACB）=90°-∠ACB，

∴当∠ACB=40°时，∠AIF=70°，

∵CF∥AD，

∴∠BFC=∠AIF=70°，

同法可得：当∠ACB=90°时，∠BFC=45°，

当∠ACB=110°时，∠BFC=35°，

故答案为70°，45°，35°；

②∵∠BFC=∠AIF=90°-∠ACB，

∴∠BFC＜90°，

∴∠BFC总是锐角；

③如图，过点作于；

结论：，

，

．