题目内容
【题目】Rt△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值为______.
【答案】![]()
【解析】
根据矩形的性质就可以得出,EF,AP互相平分,且EF=AP,根据垂线段最短的性质可以得出AP⊥BC时,AP的值最小,即AM的值最小,由勾股定理求出BC,根据面积关系建立等式求出其解即可.
∵四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点.
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵![]() AP.BC=
AP.BC=![]() AB.AC,
AB.AC,
∴AP.BC=AB.AC.
∵AB=3,AC=4,∠BAC=90°,
∴在Rt△ABC中,由勾股定理,得BC=![]() =5,
=5,
∴5AP=3×4
∴AP=![]() .
.
∴AM=![]() .
.
故答案为:![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
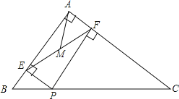
【题目】如图:已知![]() .
.

(1)读句画图:画![]() 的角平分线
的角平分线![]() 、
、![]() 交
交![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() 、
、![]() 交于点
交于点![]() ,过
,过![]() 点作
点作![]() 交
交![]() 的延长线于
的延长线于![]() .
.
(2)在(1)的条件下解决下面问题:
①填表
|
|
|
|
| __________ | ______________ | ______________ |
②根据图中的数据,你发现无论![]() 是什么角,
是什么角,![]() 总是__________(填锐角、钝角或直角).
总是__________(填锐角、钝角或直角).
③若过![]() 点作
点作![]() 于
于![]() ,你能猜想
,你能猜想![]() 与
与![]() 之间的数量关系吗?说明理由.(在(1)中的图上作
之间的数量关系吗?说明理由.(在(1)中的图上作![]() 于
于![]() )
)