题目内容
 如图,△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AE=BD.
如图,△ABC中,∠ACB=90°,AC=BC,点D在边AB上,连接CD,将线段CD绕点C顺时针旋转90°至CE位置,连接AE.求证:AE=BD.考点:旋转的性质
专题:证明题
分析:先根据旋转的性质,由线段CD绕点C顺时针旋转90°至CE位置得到CD=CE,∠DCE=90°,加上CB=CA,∠BCA=90°,于是根据旋转的定义可把△BCD绕点C顺时针旋转90°得到△ACE,然后根据旋转的性质即可得到结论.
解答:证明:∵线段CD绕点C顺时针旋转90°至CE位置,
∴CD=CE,∠DCE=90°,
∵CB=CA,∠BCA=90°,
∴△BCD绕点C顺时针旋转90°得到△ACE,
∴AE=BD.
∴CD=CE,∠DCE=90°,
∵CB=CA,∠BCA=90°,
∴△BCD绕点C顺时针旋转90°得到△ACE,
∴AE=BD.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
如果一个数的倒数是-2,那么这个数的相反数是( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
| 1 |
| 3 |
| A、3 | ||
B、
| ||
C、-
| ||
| D、-3 |
在Rt△ABC中,∠C=90°,BC=1,那么AB的长为( )
A、
| ||
| B、cosA | ||
C、
| ||
| D、sinA |
 已知线段a及∠1,用尺规作△ABC使得AC=a,AB=2a,∠A=∠1.
已知线段a及∠1,用尺规作△ABC使得AC=a,AB=2a,∠A=∠1.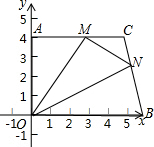 在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别是线段AC、线段BC上的动点,使得△MON的面积最大时,周长最短,则点M的坐标为
在平面直角坐标系中,直角梯形AOBC的位置如图所示,∠OAC=90°,AC∥OB,OA=4,AC=5,OB=6.M、N分别是线段AC、线段BC上的动点,使得△MON的面积最大时,周长最短,则点M的坐标为