题目内容
已知抛物线y1=ax2+bx+a(a>2)与直线y2=mx+1交于A(m,2)(m>0),B(p,q)两个不同的点,且直线AB与y轴交于点C,求△OBC面积的取值范围.
考点:二次函数的性质
专题:
分析:把点A坐标代入直线解析式求出m=1,然后代入抛物线解析式求出a、b的关系,再联立两函数解析式消掉y得到关于x的一元二次方程,然后求出点B的横坐标,再根据三角形的面积a>2进行判断即可.
解答:解:∵点A(m,2)在直线y2=mx+1上,
∴m2+1=2,
解得m1=1,m2=-1(舍去),
∴点A的坐标为(1,2),
直线解析式为y2=x+1,
代入抛物线得a+b+a=2,
∴b=2-2a,
联立
消掉y得,
ax2+(b-1)x+a-1=0,
所以,ax2+(1-2a)x+a-1=0,
解得x1=1,x2=
,
令x=0,则y=1,
所以,OC=1,
△OBC面积=
×1×
=
-
,
∵a>2,
∴
<
,
∴
-
>
-
>
,
∴
<△OBC面积<
.
∴m2+1=2,
解得m1=1,m2=-1(舍去),
∴点A的坐标为(1,2),
直线解析式为y2=x+1,
代入抛物线得a+b+a=2,
∴b=2-2a,
联立
|
ax2+(b-1)x+a-1=0,
所以,ax2+(1-2a)x+a-1=0,
解得x1=1,x2=
| a-1 |
| a |
令x=0,则y=1,
所以,OC=1,
△OBC面积=
| 1 |
| 2 |
| a-1 |
| a |
| 1 |
| 2 |
| 1 |
| 2a |
∵a>2,
∴
| 1 |
| 2a |
| 1 |
| 4 |
∴
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
∴
| 1 |
| 4 |
| 1 |
| 2 |
点评:本题考查了二次函数的性质,联立两函数解析式求交点坐标,根据一次函数图象上点的坐标特征求出m的值是解题的关键,也是本题的突破口.

练习册系列答案
相关题目
|a|+|b|=|a+b|,则a,b关系是( )
| A、a,b的绝对值相等 |
| B、a,b异号 |
| C、a+b的和是非负数 |
| D、a,b同号或其中至少一个为零 |
下列方程中,关于x的一元二次方程是( )
A、
| ||||
| B、3(x+1)2=2(x+1) | ||||
C、
| ||||
| D、2x2-3xy+y2=9 |

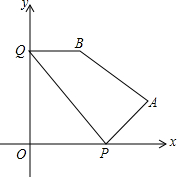 如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.
如图,在平面直角坐标系中,A点的坐标是(12,3),B点的坐标是(2,7),在x,y轴上分别有一点P和Q,若有四边形PABQ的周长最短,求周长最短的值.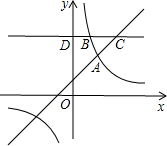 如图,一次函数y=kx+1(k≠0)与反比例函数y=
如图,一次函数y=kx+1(k≠0)与反比例函数y=