题目内容
19.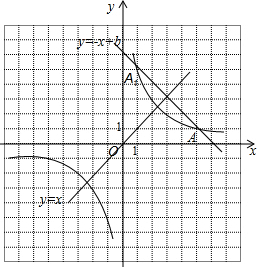 如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.根据图象写出答案.
如图,在方格纸中建立直角坐标系,已知一次函数y1=-x+b的图象与反比例函数y2=$\frac{k}{x}$的图象相交于点A(5,1)和A1.若点A和A1关于直线y=x对称.根据图象写出答案.(1)方程$\frac{k}{x}$+x-b=0的解是x=1或x=5;
(2)不等式$\frac{k}{x}$+x-b≥0的解是0<x≤1或x≥5.
分析 抛物线关于直线y=x轴对称,可证直线y1=-x+b与直线y=x互相垂直,根据轴对称性可求点A1的坐标,
(1)根据y1与y2的图象的交点坐标,求方程$\frac{k}{x}$+x-b=0的解;
(2)根据y1与y2的图象的位置关系,求得不等式$\frac{k}{x}$+x-b≥0的解集.
解答 解:由函数图象根据题意可知A1(1,5),
(1)当x=1或x=5时,y1=y2.
所以方程$\frac{k}{x}$+x-b=0的解是:x=1或x=5;
(2)当0<x≤1或x≥5时,y1≤y2,
不等式$\frac{k}{x}$+x-b≥0的解是0<x≤1或x≥5;
故答案为:x=1或x=5;0<x≤1或x≥5.
点评 本题考查了反比例函数与一次函数的交点问题.关键是结合图象的位置根据对称性求得点A1的坐标.

练习册系列答案
相关题目
11.下列计算正确的是( )
| A. | a5•a3=2a8 | B. | a3+a3=a6 | C. | 2a-2=$\frac{1}{2{a}^{2}}$ | D. | a5÷a3=a2 |
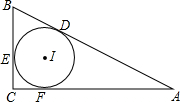 如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为30.
如图,⊙I是直角△ABC的内切圆,切点为D、E、F,若AF=10,BE=3,则△ABC的面积为30.