题目内容
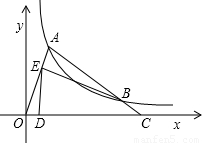
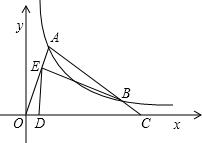 如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是________.若A点在双曲线
如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是________.若A点在双曲线 (x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是________.
(x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是________.
(5,0) 0<m<
分析:首先过点A作AH⊥x轴于点H,过点C作CF⊥OA于点F,易得△AOH∽△COF,然后由相似三角形的对应边成比例,即可求得OC的长,即可得点C的坐标;
由∠BED=∠AOC,AC=OC,易证得△ABE∽△OED,由A与C的坐标,可求得直线AC与反比函数的解析式,继而求得点B的坐标,即可求得AB的长,然后设AE=x,由相似三角形的对应边成比例,可得方程:x2- x+
x+ m=0,然后由判别式△>0,求得m的取值范围.
m=0,然后由判别式△>0,求得m的取值范围.
解答: 解:过点A作AH⊥x轴于点H,过点C作CF⊥OA于点F,
解:过点A作AH⊥x轴于点H,过点C作CF⊥OA于点F,
∵AC=OC,
∴CF⊥OA,
∴∠CFO=∠AHO=90°,
∵∠AOH=∠COF,
∴△AOH∽△COF,
∴ ,
,
∵点A坐标是(1,3),
∴OA= =
= ,
,
∴OF= OA=
OA= ,
,
∴OC= =5,
=5,
∴点C的坐标为:(5,0);
∵AC=OC,
∴∠BAE=∠AOC,
∵∠OEC=∠BED+∠OED=∠BAE+∠ABE,∠BED=∠AOC,
∴∠OED=∠ABE,
∴△ABE∽△OED,
∴AE:OD=AB:OE,
设AE=x,则OE= -x,
-x,
∵点A(1,3),点C(5,0),
∴设直线AC的解析式为:y=kx+b,
即 ,
,
解得: ,
,
即y=- x+
x+ ①,
①,
∵点A在反比例函数图象上,
∴此反比例函数的解析式为:y= ②,
②,
联立①②得:x=4或x=1(舍去),
∴点B的坐标为:(4, ),
),
∴AB= =
= ,
,
∴x:m= :(
:( -x),
-x),
即x2- x+
x+ m=0,
m=0,
∵线段OA上符合条件的点E有且仅有2个,
∴判别式△=(- )2-4×1×
)2-4×1× m=10-15m>0,
m=10-15m>0,
解得:m< ,
,
∵点E是线段OA上一点(不与O,A重合),
∴m>0,
∴m的取值范围是:0<m< .
.
故答案为:(5,0);0<m< .
.
点评:此题考查了待定系数法求一次函数与反比例函数的解析式、相似三角形的判定与性质、等腰三角形的性质、三角形外角的性质以及判别式的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

分析:首先过点A作AH⊥x轴于点H,过点C作CF⊥OA于点F,易得△AOH∽△COF,然后由相似三角形的对应边成比例,即可求得OC的长,即可得点C的坐标;
由∠BED=∠AOC,AC=OC,易证得△ABE∽△OED,由A与C的坐标,可求得直线AC与反比函数的解析式,继而求得点B的坐标,即可求得AB的长,然后设AE=x,由相似三角形的对应边成比例,可得方程:x2-
 x+
x+ m=0,然后由判别式△>0,求得m的取值范围.
m=0,然后由判别式△>0,求得m的取值范围.解答:
 解:过点A作AH⊥x轴于点H,过点C作CF⊥OA于点F,
解:过点A作AH⊥x轴于点H,过点C作CF⊥OA于点F,∵AC=OC,
∴CF⊥OA,
∴∠CFO=∠AHO=90°,
∵∠AOH=∠COF,
∴△AOH∽△COF,
∴
 ,
,∵点A坐标是(1,3),
∴OA=
 =
= ,
,∴OF=
 OA=
OA= ,
,∴OC=
 =5,
=5,∴点C的坐标为:(5,0);
∵AC=OC,
∴∠BAE=∠AOC,
∵∠OEC=∠BED+∠OED=∠BAE+∠ABE,∠BED=∠AOC,
∴∠OED=∠ABE,
∴△ABE∽△OED,
∴AE:OD=AB:OE,
设AE=x,则OE=
 -x,
-x,∵点A(1,3),点C(5,0),
∴设直线AC的解析式为:y=kx+b,
即
 ,
,解得:
 ,
,即y=-
 x+
x+ ①,
①,∵点A在反比例函数图象上,
∴此反比例函数的解析式为:y=
 ②,
②,联立①②得:x=4或x=1(舍去),
∴点B的坐标为:(4,
 ),
),∴AB=
 =
= ,
,∴x:m=
 :(
:( -x),
-x),即x2-
 x+
x+ m=0,
m=0,∵线段OA上符合条件的点E有且仅有2个,
∴判别式△=(-
 )2-4×1×
)2-4×1× m=10-15m>0,
m=10-15m>0,解得:m<
 ,
,∵点E是线段OA上一点(不与O,A重合),
∴m>0,
∴m的取值范围是:0<m<
 .
.故答案为:(5,0);0<m<
 .
.点评:此题考查了待定系数法求一次函数与反比例函数的解析式、相似三角形的判定与性质、等腰三角形的性质、三角形外角的性质以及判别式的性质.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )
如图,在⊙O中,OA⊥BC,∠AOC=50°,则∠ADB的度数为( )| A、15° | B、20° | C、25° | D、50° |
 如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,∠AOC=60°,则∠B=
如图,在⊙O中,AB为⊙O的直径,弦CD⊥AB,∠AOC=60°,则∠B= (2013•浙江一模)如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是
(2013•浙江一模)如图,在△AOC中,AC=OC,O是坐标原点,点C在x轴上,点A坐标是(1,3),则点C的坐标是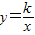 (x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是 .
(x>0)上,AC与双曲线交于点B,点E是线段OA上一点(不与O,A重合),设点D(m,0)是x轴正半轴上的一个动点,且满足∠BED=∠AOC,当线段OA上符合条件的点E有且仅有2个时,m的取值范围是 .