题目内容
16．化简分式：$\frac{{x}^{2}+3x+2}{{x}^{2}+2x+1}$÷[$\frac{x+2}{2x-1}$（$\frac{1-2x}{3x+6}$+4x-2）+$\frac{1}{3}$]．分析 根据分式混合运算的法则进行计算即可．
解答 解：原式=$\frac{（x+1）（x+2）}{（x+1）^{2}}$÷[$\frac{x+2}{2x-1}$•$\frac{-（2x-1）}{3（x+2）}$+$\frac{x+2}{2x-1}$•2（2x-1）+$\frac{1}{3}$]
=$\frac{x+2}{x+1}$÷[-$\frac{1}{3}$+2（x+2）+$\frac{1}{3}$]
=$\frac{x+2}{x+1}$÷2（x+2）
=$\frac{x+2}{x+1}$•$\frac{1}{2（x+2）}$
=$\frac{1}{2（x+1）}$．
点评 本题考查的是分式的化简求值，熟知分式混合运算的法则是解答此题的关键．
练习册系列答案
相关题目
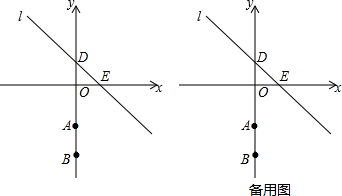
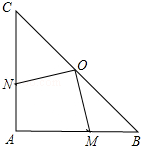如图，在Rt△ABC中，∠A=90°，AB=AC=4cm，若O是BC的中点，动点M在AB移动，动点N在AC上移动，且AN=BM．