题目内容
解下列分式方程
① ;
;
② .
.
解:① ,
,
将方程变形,得
 +
+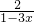 =
= ,
,
 =
= ,
,
3(1-3x)=3×2,
去括号,得
3-9x=3×2,
移项,合并同类项,得
-9x=3,
系数化为1,得
x=- .
.
检验:将x=- 代入原方程.1-3x≠0,
代入原方程.1-3x≠0,
∴原方程的解为:x= ;
;
② .
.
将方程通分,得
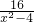 -
- =
= ,
,
去分母,得
16+(x-2)2=(x+2)2,
去括号,得
16+x2-4x+4=x2+4x+4,
移项,合并同类项,得
-8x=-16,
系数化为1,得
x=2.
检验:x=2时,x2-4=0,x=2不是原分式方程的解.
原分式方程无解.
分析:①将方程变形,得 +
+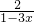 =
= ,整理后得3(1-3x)=3×2,再去括号,移项,合并同类项,然后将系数化为即可求解;
,整理后得3(1-3x)=3×2,再去括号,移项,合并同类项,然后将系数化为即可求解;
②将方程通分,得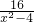 -
- =
= ,然后去分母,去括号,移项,合并同类项,然后将系数化为即可求解.
,然后去分母,去括号,移项,合并同类项,然后将系数化为即可求解.
点评:此题主要考查学生对解分式方程的理解和掌握,解答此题时,关键是将方程变形找到比较简便的解法.另外解分式方程一定注意要验根.
 ,
,将方程变形,得
 +
+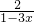 =
= ,
, =
= ,
,3(1-3x)=3×2,
去括号,得
3-9x=3×2,
移项,合并同类项,得
-9x=3,
系数化为1,得
x=-
 .
.检验:将x=-
 代入原方程.1-3x≠0,
代入原方程.1-3x≠0,∴原方程的解为:x=
 ;
;②
 .
.将方程通分,得
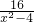 -
- =
= ,
,去分母,得
16+(x-2)2=(x+2)2,
去括号,得
16+x2-4x+4=x2+4x+4,
移项,合并同类项,得
-8x=-16,
系数化为1,得
x=2.
检验:x=2时,x2-4=0,x=2不是原分式方程的解.
原分式方程无解.
分析:①将方程变形,得
 +
+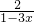 =
= ,整理后得3(1-3x)=3×2,再去括号,移项,合并同类项,然后将系数化为即可求解;
,整理后得3(1-3x)=3×2,再去括号,移项,合并同类项,然后将系数化为即可求解;②将方程通分,得
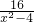 -
- =
= ,然后去分母,去括号,移项,合并同类项,然后将系数化为即可求解.
,然后去分母,去括号,移项,合并同类项,然后将系数化为即可求解.点评:此题主要考查学生对解分式方程的理解和掌握,解答此题时,关键是将方程变形找到比较简便的解法.另外解分式方程一定注意要验根.

练习册系列答案
相关题目